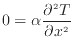• 学問 -top-

1. 概要

温度分布や速度分布を求めることにより、伝熱量や摩擦力を知ることができる。現象を記述する式(支配方程式)が分かっていて知りたい条件での境界条件、初期条件で解くことが出来れば、温度分布や速度分布の厳密解を求められる。

支配方程式が微分方程式である場合、解く際の積分定数を求めるために、それぞれの変数の微分の階数を足し合わせた数だけ条件が必要である。時間微分の場合は初期条件、位置での微分であれば境界条件と呼ばれる。一つの例として、１次元の熱伝導の定常の現象の厳密解を求めよう。この時、支配方程式は以下の１次元の熱伝導方程式となる。

$$0 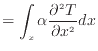= \alpha \frac{\partial ^2 T}{\partial x^2}$$ (1.1)

$x = 0、x = 7$ を境界とし、境界条件を以下の２条件とする。

$$x = 0でT = 10℃$$ (1.2)

$$x = 7でT = 30℃$$ (1.3)

式(1.1)を$x$ で積分して、

$$= \int_x \alpha \frac{\partial ^2 T}{\partial x^2} dx$$ 0

$$= \alpha \frac{\partial T}{\partial x} + C_1$$ 0

さらに$x$ で積分すると、

$$= \int_x \alpha \frac{\partial T}{\partial x} dx + \int_x C_1 dx$$ 0

$$= \alpha T + C_1 x + C_2$$ 0

境界条件より、 $C_2 = - 10 \alpha$ と $C_1 = - \dfrac{20}{7} \alpha$ となる。よって、温度は次の関数となる。

$$T = \frac{20}{7} x + 1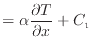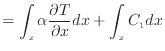0$$

上式をxで微分するとフーリエの法則より熱流束$q$ は次のように求められる。

$$q= - k \frac{\partial T}{\partial x} = - \frac{20}{7} k$$

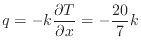
このように厳密解を求めることができるが、多くの場合、支配方程式と条件から厳密解を求めることは難しい。そこで数値計算では、計算対象を細かな領域に分割して(離散化)、温度分布や速度分布の連続的な値を求めれるのではなく、分割した不連続な点(離散点)における値を求める。

離散化により、対象を分けた不連続な点ごとの未知数の数と同じ数の方程式を立て、連立させ解くことにより、それぞれの点での値を求める。離散化では、支配方程式と境界条件(非定常の現象では初期条件)を離散化する。また、位置での離散化に加え非定常では時間で離散化する。

計算の流れは以下の通りである。

1. 求めたい現象の支配方程式と境界条件、初期条件を求める
2. 離散化する（支配方程式・境界条件・初期条件を領域と時間で離散化）
3. 離散化した式（連立方程式）を解く

ここでは支配方程式（保存式）として以下を考えていく。

質量保存式

運動量保存式

　速度の計算

エネルギー保存式

　温度の計算

化学種保存式

　濃度（質量分率・モル分率）の計算

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。