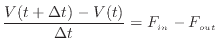


Next: 2.1.2 支配方程式
Up: 2.1 保存量
Previous: 2.1 保存量
2.1.1 保存の関係
支配方程式では、知りたい物理量に関する保存式を立てる。支配方程式はそれぞれ、保存を考えるコントロールボリューム(境界領域)について考える。例として図2.1のような排出口のある水槽をコントロールボリューム(境界領域)として水の体積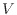 [m
[m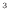 ]の保存を考えてみる。ある時間
]の保存を考えてみる。ある時間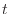 [s]での水の体積を
[s]での水の体積を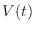 [m
[m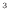 ]、
]、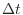 [s]後の水の体積を
[s]後の水の体積を
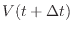 [m
[m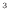 ]と表す。
]と表す。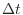 [s]間で変化する水槽の水の体積は、入ってくる水の流量
[s]間で変化する水槽の水の体積は、入ってくる水の流量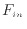 [m
[m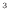 /s]と出ていく水の流量
/s]と出ていく水の流量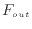 [m
[m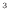 /s]に経過時間
/s]に経過時間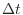 [s]を掛けて次の関係で表される。
[s]を掛けて次の関係で表される。
両辺を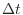 で割ると次式となる。
で割ると次式となる。
左辺は"水槽に入ってる量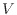 [m
[m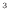 ]の
]の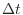 [s]での変化量"となる。
ここで時間の変化
[s]での変化量"となる。
ここで時間の変化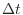 [s]が限りなく小さい場合には次式となる。
[s]が限りなく小さい場合には次式となる。
上式の左辺は水槽の水量の時間変化、右辺は出入りする水の流量である。
水槽が密閉されており中の水の様子が観察できない場合でも、上式に水の流入量と流出量を代入することにより、水の体積の変化を知ることができる。
図 2.1:
Control Volume Water
|
|



Next: 2.1.2 支配方程式
Up: 2.1 保存量
Previous: 2.1 保存量
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。