


Next: A.1.3 の計算
Up: A.1 数学的な説明補足
Previous: A.1.1 微分の定義
関数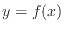 と関数
と関数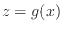 の積を
の積を で微分すると、微分の定義より以下のようになる。
で微分すると、微分の定義より以下のようになる。
左辺が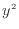 の場合は、上式において
の場合は、上式において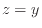 とすれば以下のようになる。
とすれば以下のようになる。
上式で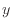 ではなく、ベクトル
ではなく、ベクトル
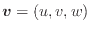 であると、次のようになる。
であると、次のようになる。
関数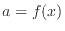 と関数
と関数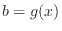 と関数
と関数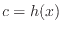 の積の微分を式(A.1)から求める。
の積の微分を式(A.1)から求める。



Next: A.1.3 の計算
Up: A.1 数学的な説明補足
Previous: A.1.1 微分の定義
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
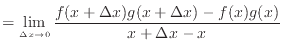
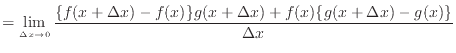
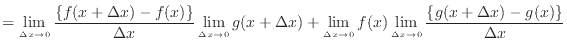
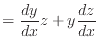
![]() の場合は、上式において
の場合は、上式において![]() とすれば以下のようになる。
とすれば以下のようになる。
![]() ではなく、ベクトル
ではなく、ベクトル
![]() であると、次のようになる。
であると、次のようになる。
![]() と関数
と関数![]() と関数
と関数![]() の積の微分を式(A.1)から求める。
の積の微分を式(A.1)から求める。