全微分と偏微分

一変数関数

温度 T が時間 t のみの関数 T ( t ) である時、温度 T の時間変化は微分の形で表せ、微分は次式で定義される。

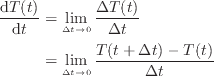
$\ddif{T(t)}{t} &= \lim_{\Delta t \to 0} \frac{\Delta T(t)}{\Delt......&= \lim_{\Delta t \to 0} \frac{T(t + \Delta t) - T(t)}{\Delta t}$

一変数関数では偏微分は定義されない。

多変数関数

温度 T がそれぞれ独立な時間 t 、座標 x 、 y 、 z の関数 T ( t, x, y, z ) である時、ある決まった座標（ x 、 y 、 z が一定）での温度 T の時間変化は偏微分の形で表される。偏微分は次式で定義される。

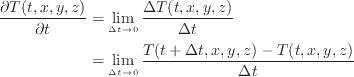
$\pdif{T(t, x, y, z)}{t} &= \lim_{\Delta t \to 0} \frac{\Delta T(...... t \to 0} \frac{T(t + \Delta t, x, y, z) - T(t, x, y, z)}{\Delta t}$

多変数関数での全微分 dT ( t, x, y, z ) は全ての変数の微小変化に対する変化量として定義される。

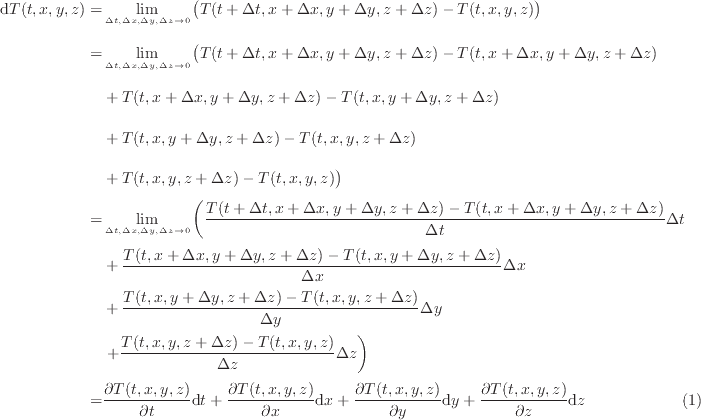
$\dif T(t, x, y, z) =& \lim_{\Delta t, \Delta x, \Delta y, \Delta ...... x + \pdif{T(t, x, y, z)}{y} \dif y + \pdif{T(t, x, y, z)}{z} \dif z$

この式(1)の両辺を dt で割れば次のように一変数関数と同様の形に変形できる。

$\ddif{T(t, x, y, z)}{t} = \pdif{T(t, x, y, z)}{t} + \pdif{T(t, x......T(t, x, y, z)}{y} \ddif{y}{t} + \pdif{T(t, x, y, z)}{z} \ddif{z}{t}$

しかし、ここでそれぞれの変数 t 、 x 、 y 、 z は独立な変数（お互いにどんな関係性もない変数）であるので、 dx / dt 、 dy / dt 、 dx / dt は意味を持たない（特定の値を持つことはない）ため、このような変形も意味を持たない。

関数 T ( t, x, y, z ) は任意の時間、任意の位置での温度を表している。時間、座標に対する温度の変化が全て分かれば関数 T ( t, x, y, z ) の形が分かる。例えば、現実ではまずありえない変化ではあるが、温度が時間とそれぞれの座標に対して単調に変化するとし、次式で表されるとする。

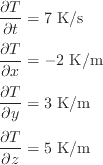
$\pdif{T}{t} &= 7 \text{ K/s}\pdif{T}{x} &= - 2 \text{ K/m}\pdif{T}{y} &= 3 \text{ K/m}\pdif{T}{z} &= 5 \text{ K/m}$

これを式(1)へ代入する。

$\dif T(t, x, y, z) = 7 \dif t - 2 \dif x + 3 \dif y + 5 \dif z$

両辺を積分する。

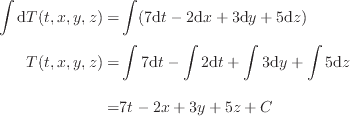
$\int \dif T(t, x, y, z) =& \int (7 \dif t - 2 \dif x + 3 \dif y ......t + \int 3 \dif y + \int 5 \dif z=& 7 t - 2 x + 3 y + 5 z + C$

ここで C は積分定数で、ある状態の温度が分かれば値が求まる。例えば t = 0 、x = 1 、 y = 2 、 z = 2 での温度が T = 4 であれば、 C = -10 であることが分かり、 T = 7 t - 2 x + 3 y + 5 z - 10 である。変化量（偏微分の値）ではある基準からの変化しか求められないため、必ず基準が必要となる。このように、それぞれの変数に対する変化を合わせることで温度の関数を知ることが出来る。

より詳しい内容を学びたい人にはスミルノフ高等数学教程 I巻[第一分冊], スミルノフ, 共立出版, 1958.を薦める。

2015年7月24日　椿耕太郎

全微分と偏微分

一変数関数

多変数関数

関連する記事