圧力

定義

圧力とはある面にかかる面積当たりの力である。単位はPa（パスカル）であり、式で表すと圧力 P [Pa]は面にかかる力 F [N]と面積 A [m²]で次のように表される。

$P = \dfrac{F}{A}$

単位は国際単位系（SI）でPaと決められている。身の回りでは天気予報などで大気圧を示す際に使われる10²を表すh（ヘクト）をつけたhPaや、高圧ガスの圧力を示す際に使われる10⁶を表すM（メガ）をつけたMPaとして表されている。大気圧は約1000 hPa（= 0.1 MPa = 100 kPa）である（気候により大気圧の値は変わるが、標準大気圧は101 325 Paと定義されている[1]）。他に国際単位系（SI）ではないが習慣的に圧力を高さで表す場合がある（高さで表す場合ヘッドと呼ばれ、水の高さの場合、水頭とも呼ばれる）。よく用いられるものに水銀の高さで表したmmHg（Torrとも表される）、水の高さで表したmmH₂Oがある。

圧力を高さで表す

なぜ高さで圧力を表せるのだろうか。水銀を使った気圧計を例に高さと圧力の関係をみてみる。試験管のような片方のふさがれた十分に長い筒状の容器を水銀で満たし、その容器を図1に示すようにふさがれた側を上にして容器の下端が下に置いた広い容器の中につかるように立てる。容器の中の水銀には二つの力が働く。容器の中の水銀には重力が働いているので、落ちようとする下向きの力が働く。また、水銀と大気の接触面では大気が水銀を押す力が働き、容器下部で容器内の水銀を上向きに押す。

図 1　水銀柱

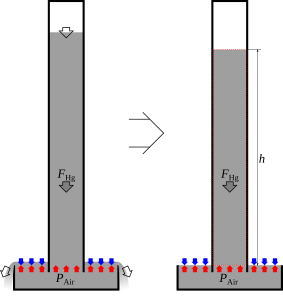
水銀に働く力をそれぞれ考えてみる。容器内の水銀に重力により働く力 F_Hg [N]は筒状容器内の水銀の質量 m_Hg [kg]と重力加速度 g [m/s²]の積で次式で表される。

$F_\text{Hg} = g m_\text{Hg}$

(1)

ここで水銀の質量 m_Hg [kg]を水銀の密度ρ_Hg [kg/m³]と筒状容器の断面積 A [m²]、筒状容器内の水銀の高さ h [m]で表すと次式となる。

$m_\text{Hg} = \rho_\text{Hg} A h$

(2)

上式(2)を式(1)へ代入する。

$F_\text{Hg} &= \rho_\text{Hg} A g h$

(3)

このF_Hgが水銀に重力による働く力の大きさである。次に大気が水銀を押す力 F_Air を求める。大気圧を P_Air とおけば次式となる。

$F_\text{Air} = A P_\text{Air}$

(4)

容器が十分に長く、大気圧による力より水銀の重さによる力が大きい（F_Hg > F_Air）と、大気の押す力より水銀が押す力が大きいので、水銀は動きだし容器からあふれる。容器の中の水銀は下に動き、容器の上端では水銀の面と容器の壁との間に空間が生じる（この空間は何も入ってこないため、ほぼ真空となりトリチェリの真空と呼ばれるが、厳密には水銀が僅かに蒸発するため気体の水銀が存在する。水銀の蒸気圧は25 ℃で0.245 Paである[2]）。容器の中の水銀があふれ、容器中の水銀の高さ h が減ることで水銀の重さによる力は徐々に小さくなる。あふれる量も少なくなっていき、大気圧による力と水銀の重さによる力が釣り合ったら水銀は動かなくなる（図 1）。この釣り合った状態で、水銀の重さによる力と大気圧による力が等しくなっている。そのため水銀の高さを測ることで大気圧を計ることが出来る。水銀の重さによる力と大気圧による力が釣り合っており、式(3)(4)より

$F_\text{Hg} &= F_\text{Air} \\\rho_\text{Hg} g h &= P_\text{Air}$

となる。ここで水銀の密度ρ_Hg の値にρ_Hg = 13 595.1 kg/m³ （大気圧、0 ℃）[2]、標準重力加速度g = 9.806 65 m/s² [2]（重力加速度は場所によって違い、標準値は国際単位系SI[1]で定められている。日本の京都大学地質学鉱物学教室重力室で計られた値は標準値よりも小さく9.797 072 7 m/s²である[2]）を用いると、

$P_\text{Air} &= 13\ 595.0 \text{ kg/m$^3$} \times 9.806\ 65 \text......h \nonumber \\&= 133\ 322.3874 \text{ kg/(m$^2$\ s$^2$)} \times h$

となり、水銀の高さ h を測り約133 322倍（高さの単位がmmであれば133倍）すると大気の圧力 P_Air [Pa]を求めることができる。圧力の単位にmmHgを用いればmmで表した h の値から次式のようにそのまま圧力mmHgを求められる。

$P_\text{Air} / \text{mmHg} = h / \text{mm}$

このように高さで圧力を計る圧力計はマノメーターと呼ばれている。

圧力差を表す

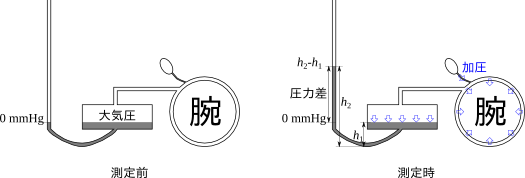
密閉された容器に水銀を入れることで大気圧を水銀の高さで表すことが出来た。同様の原理で圧力差も水銀の高さで表すことが出来る。図2に示すようなmmHgで表されることの多い血圧を計る水銀血圧計を例にとる。測定前は水銀の両端とも大気に解放されており大気圧 P_Air であるため、水銀の高さは同じである。この高さが腕に圧力のかかっていない基準の0 mmHgである。血圧測定時に腕側に空気を送り込んで腕に P_Meaの圧力を掛けると、水銀が押され水銀面の高さに差が生じる。腕側には大気圧 P_Air に加え P_Mea の圧力が掛かっている。この時の下端の折り返しの位置での力の釣り合いを考える。目盛側の大気圧 P_Air と水銀の高さh₂、腕側の圧力（P_Mea + P_Air）と水銀の高さh₁で釣り合っており、力の釣り合いは次式で表される。

$(P_\text{Air} + \rho_\text{Hg} g h_2) A &= (P_\text{Mea} + P_\tex......g h_1) A \nonumber \\\rho_\text{Hg} g (h_2 - h_1) &= P_\text{Mea}$

この高さの差 (h₂ - h₁)から腕に加えられた圧力 P_Mea を求めることが出来る（このとき腕側の水銀面の断面積を十分に大きくすれば、移動する水銀の体積に対する腕側の高さの変化が測定側の高さの変化に比べ小さな値になるため、測定での誤差はほとんど生じない。例えば測定側の直径を1 mm、腕側の直径を10 mmとすると、断面積はそれぞれ 0.25 mm²、25 mm²と100倍違うため、腕側の高さの変化は100分の一となるため影響は十分に小さい）。圧力の単位をmmHg、高さをmmで表せば式(6)は次式となり、目盛の値 (h₂ - h₁)/mmが腕に加えた圧力となる。

$(h_2 - h_1) /\text{mm}= P_\text{Mea} /\text{mmHg}$

図 2　血圧計

-おまけ- 十分に長くない容器

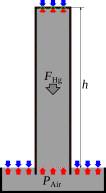
容器が十分に長くない場合には、水銀の質量による下向きの力 F_Hgが大気圧による上向きの力 F_Air 以下（F_Hg ? F_Air）であれば（図3）、容器内の水銀に上向きの力が働く。容器の上端が塞がっているので、水銀は容器の上端の壁を F_Air - F_Hg の力で押す。上端の壁は水銀側（下側）から (F_Air - F_Hg) の力を受け、大気側（上側）からは F_Air の力を受ける。上と下の力は壁の弾性力と釣り合う。壁は水銀を押すことはできるが、引くことはできない。そのため (F_Air - F_Hg) （大気圧による力ー上端の壁の弾性力）は必ず正の値となる。上端に働く力F_Topは次式で表される。

$F_{Top} = F_\text{Air} - F_\text{Hg} = A (P_\text{Air} - P_\text{Hg}) = A (P_\text{Air} - \rho_\text{Hg} g h)$

水銀は容器に押し込まれ高さから圧力を測ることが出来ない。

図 3　十分に長くない容器での水銀柱

-おまけ- mmHgの定義

mmHgの定義は標準大気圧101 325 Pa[1]を760 mmHgとしている。

$760 \text{ mmHg} &\equiv 101\ 325 \text{ Pa} \text{ mmHg} &\simeq 133.322 \text{ Pa}$

また、式(5)の h の単位をmではなくmmで表すと、1 mmHg ? 133.322 Paであることが分かる（非SI単位として国際単位系SIで定義されている[1]）。 SIで定められた標準大気圧101 325 Paは、大気圧0 ℃における水銀密度とSIで定められた標準重力加速度9.806 65 m/s²での水銀柱 760 mmの値と非常に近い値である。

参考文献

1 （独）産業技術総合研究所計量標準総合センター, 国際文章第8版(2006) 国際単位系（SI）, 2006, pdfデータ.

2 国立天文台, 理科年表, 丸善出版, 2014.

2015年8月24日　椿耕太郎

圧力

定義

圧力を高さで表す

圧力差を表す

-おまけ- 十分に長くない容器

-おまけ- mmHgの定義

参考文献

関連する記事