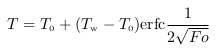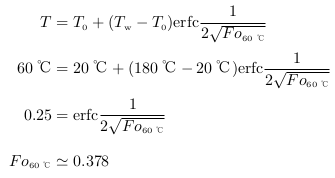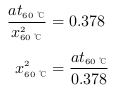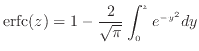熱伝導率と熱拡散率(温度伝導率)の違い
違いの分かりにくい熱伝導率と熱拡散率(温度伝導率)についてそれぞれ詳しくみていく。
熱伝導率 Thermal conductivity(単位:W/(m K))と熱拡散率(温度伝導率、熱拡散係数、温度拡散率とも呼ばれる) Thermal diffusivity(単位: m/s2)はともに物質と状態が決まれば値が決まる物性値である脚注1。
脚注1 流体(気体と液体)の粘性を表す粘性係数(粘度) Dynamic viscosityと動粘性係数(動粘度) Kinematic viscosityの関係に近い。
1 熱伝導率と熱拡散率の定義
熱伝導率 k (単位: W/(m K))は次式で表されるフーリエの法則で定義される。
熱流束
q(単位: W/m
2)
脚注2と温度勾配∂
T/∂
x(単位: K/m )
脚注3の関係において、熱伝導率 k (単位: W/(m K))が熱の伝わりやすさを示す。
熱拡散率
a(単位: m
2/s)は熱伝導率
k(単位: W/(m K))を比熱
cp(単位: J/(kg K))と密度
ρ(単位: kg/m
3)で割ることで求められる。
脚注2 伝わる面積を掛ければ伝熱量 (単位: W)が得られる。
脚注3 x方向のみの一次元の場合
2 熱伝導率と熱拡散率の関係
熱拡散率は式 (1) の定義からでは、どのような意味を持つ値なのかがわかりにくい。熱伝導率と熱拡散率(温度伝導率)の関係を想像しやすいように、熱と温度を水槽に貯まる水の量と水位に例える。図 1 のように細長い水槽が並んでいて左から水が入り、水槽の間の壁には穴があいていて隣の水槽に水が流れ込む水槽の列を考える。流れてくる水の量が伝熱量(伝わる熱の量)に、水槽の水位の変化が温度の変化に対応する。水槽の奥行きが密度ρ(単位: kg/m3)×比熱cp(単位: J/(kg K))に対応し、奥行きが深いと水が貯まっても水位は変化しづらい(密度×比熱が大きいと熱が伝わっても温度が変わりにくい)。温度差が増えると伝わる熱の量も増えるように、水位の差が大きいと流れ込む水の量も増える。
![\includegraphics[width=100mm]{figures/tank.eps}](ThermalDiffusivity20190523Fig01.png)
図1 水槽での比喩
熱伝導率は温度差(温度勾配)に対しての熱の伝わりやすさであり、水槽で考えると水位差に対してどれだけ水が流れ込むか、すなわち水槽の間の穴の数(大きさ)となる。それに対して熱拡散率(温度伝導率)は熱伝導率を密度×比熱で割った値であり温度の伝わりやすさを表す。水槽であれば水位の変わりやすさであり、穴の数(大きさ)を水槽の奥行きで割った値である。穴の数が多くても水槽の奥行きが深ければ、水が多く流れ込んでも水位の変化が小さい、すなわち熱伝導率が大きくても密度×比熱が大きければ温度変化は小さい。
3 熱拡散率の意味
より詳しく熱拡散率(温度伝導率) a (単位: m2/s)の意味を考えていき、等温面の伝わる速さを表すことを示す。大きな塊の固体の片面を一定温度で加熱した場合の、固体内の温度の伝わりと熱拡散率との関係を考えてみよう。大きな肉の塊を加熱されたフライパンで焼くことを想像してもよい(図 2 )脚注 4 。加熱された固体内部の温度の変化と熱拡散率との関係を見てみよう。まず温度分布を計算する。固体は加熱を始めるまでは温度はT0で一定で、温度がTwで加熱されるとする。経過時間 t (単位: s)は加熱開始を t = 0 s とし、加熱面から垂直に座標 x (単位: m )をとり加熱面を x = 0 m とする。この加熱される固体内の、等温面の動きを見ることで熱拡散率の意味が分かってくる。固体内の温度分布は次式のように余誤差関数 erfc脚注 5で表される(詳細な導出はpdf文末の付録 A に示す)。
上式の
T は√(
at)/
x の関数となっており、固体内の任意の位置
x と時間
t での温度が分かる。
肉を焼く例で具体的に計算してみる(図 2 )。肉は初め室温で T0 = 20 °C、フライパンと肉の接触面は Tw = 180°Cで加熱されるとする。肉をフライパンに置いた時間が t = 0 s 、フライパンと肉の接触面が x = 0 m となる。式(2) から肉の塊(熱拡散率 a = 1.3 × 10-7 m2/s )を加熱した際の加熱直後、1分後、2分後、3分後、4分後、5分後の温度分布をそれぞれ赤線で図3に示す。どの時刻でも左側のフライパン表面近くで温度が高く、離れるにつれて温度が下がる。また、図中で肉に火の通る(変性する)60 ℃の位置を赤丸で示した。1分後の温度分布を見ると、4 mm程度までは60 ℃より温度が高く火が通っていることが分かる。比較のため、同様に熱拡散率が通常の三倍の赤い肉脚注6(熱拡散率 a = 3.9 × 10-7 m2/s )での温度分布を図4に示す。熱拡散率が三倍の赤い肉では、ある位置のある温度に達するまでの時間は三分の一となる。例えば、1 cmの厚さが火が通る(60 ℃を越える)までの時間は通常の肉では4分51秒(291 s)(図3中青印)だが、三倍肉ではその三分の一の1分17秒(77 s)(図4中青印)となる。
![\includegraphics[width=100mm]{figures/meat.eps}](ThermalDiffusivity20190523Fig02.png)
図2 肉の加熱
![\includegraphics[width=70mm]{figures/temperaturedistribution1.eps}](ThermalDiffusivity20190523Fig03.png)
図3 温度分布(熱拡散率
a = 1.3 × 10
-7 m
2/s )
![\includegraphics[width=70mm]{figures/TemperatureDistribution3.eps}](ThermalDiffusivity20190523Fig04.png)
図4 温度分布(熱拡散率
a = 3.9 × 10
-7 m
2/s )
ある位置である温度となるまでの時間と熱拡散率との関係は無次元数であるフーリエ数Fo を使うと分かりやすい。式(2)のT は√(at)/x の関数となっており、これを2乗したat/x2 は無次元数でフーリエ数Fo = at/x2 と呼ばれる。上式(2)をフーリエ数Fo を使って表すと次式となる。
上式中で右辺の変数は
Fo のみであり、固体内の温度
T はフーリエ数
Fo のみの関数となっている。つまり、ある値の温度に対してはある一つの値のフーリエ数が対応する。このフーリエ数を使って、図3、図4で赤丸で示した肉の塊を焼く際にどこまで火が通るかを計算してみよう。肉は60 ℃で焼ける(変性する)ので、
Tw = 180 ℃、
T0 = 20 ℃で
T = 60 ℃になるフーリエ数
Fo60 ℃ は式(3)より次のように求められる
脚注7。
上式の
Fo が約0.378となる肉の温度60 ℃の条件を、
Fo = √(
at)/
x(時間
t 、位置
x)で書き直すと次式となる。
上式から肉の中を60 ℃の等温面がどのように移動するかが分かる。図3 の赤丸と比べてみよう。普通の肉(熱拡散率
a = 1.3 × 10
-7 m
2/s )で1分後(t
60 ℃ = 60 s)を式(4) に代入すると、位置x
60 ℃が4.38 × 10
-3 m と図中の赤丸と同じ値が求められる。他の時間でも、どの位置まで60 ℃となっているかが同様に求められる。三倍の赤い肉でも熱拡散率
a = 3.9 × 10
-7 m
2/s を代入するとこで、同様に任意の時間での60 ℃となっている位置が求めら
れる。つまり、式(4) で表されるように熱拡散率は等温面がある時間(t
60 ℃)経過した際にどれくらい進んでいるか(x
60 ℃)を表しており、温度面の移動する速度を表しているとも考えられる。熱拡散率に応じて等温面(温度)の伝わる(伝導)速さが変化する
脚注8。このことから温度伝導率とも呼ばれる。ただし、熱拡散率は式(4)で表されるように、距離÷時間ではなく距離の二乗÷時間である。等温面の移動距離の二乗と経過時間の関係が比例関係(式(4))となり、その比例定数が熱拡散率である。そのため、熱拡散率の単位は距離の二乗を時間で割った次元[m
2/s]で表される。
脚注4 焼き始めてからしばらく、肉が焼け加熱されていない面の温度が変化を始めるまでは、十分に大きな塊として扱うことができる。
脚注5 余誤差関数は次式で定義される関数である。
脚注6 専用の肉
脚注7 余誤差関数erfcは表計算ソフトなどで簡単に値を求めることができる。
脚注8 60 ℃以外の等温面の位置を求めたい場合には定数0.4067ではなく、式(3)から求めたい温度のフーリエ数を計算する。
2019年5月24日 椿 耕太郎
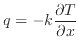
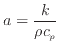
![\includegraphics[width=100mm]{figures/tank.eps}](ThermalDiffusivity20190523Fig01.png)
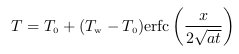
![\includegraphics[width=100mm]{figures/meat.eps}](ThermalDiffusivity20190523Fig02.png)
![\includegraphics[width=70mm]{figures/temperaturedistribution1.eps}](ThermalDiffusivity20190523Fig03.png)
![\includegraphics[width=70mm]{figures/TemperatureDistribution3.eps}](ThermalDiffusivity20190523Fig04.png)