二相状態での平均密度

二相状態での乾き度と液相と気相の密度から全体の平均密度を求める。

液相の質量をM_l [kg]、気相の質量をM_v [kg]とすると乾き度x は次式で定義される。

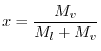
$\displaystyle x = \dfrac{m_v}{m_l + m_v}$

上式を変形して、

$\displaystyle x (m_l + m_v)$

$\displaystyle = m_v$

$\displaystyle m_l + m_v$

$\displaystyle = \dfrac{m_v}{x}$

$\displaystyle m_l$

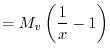
$\displaystyle = m_v \left( \dfrac{1}{x} - 1 \right)$

(1)

液相と気相が混合した状態での平均密度ρ_ave [kg/m³]を求める。平均密度は全体の質量M_all [kg]を全体の体積V_all [m³]で割ることで求められる。ここで液相の体積はV_l [m³]、気相の体積はV_v [m³]である。

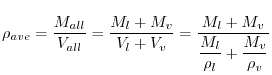
$\displaystyle \rho_{ave} = \dfrac{m_{all}}{v_{all}} = \dfrac{m_l + m_v}{v_l + v_v} = \dfrac{m_l + m_v}{\dfrac{m_l}{\rho_l} + \dfrac{m_v}{\rho_v}}$

式(1)を代入し

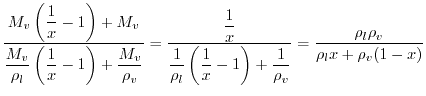
$\displaystyle \dfrac{m_v\left( \dfrac{1}{x} - 1 \right) + m_v}{\dfrac{m_v}{\rho...... \right) + \dfrac{1}{\rho_v}} = \dfrac{\rho_l \rho_v}{\rho_l x + \rho_v (1-x)}$

まとめると

$\displaystyle \rho_{ave} = \dfrac{\rho_l \rho_v}{\rho_l x + \rho_v (1-x)}$

となる。

2012年12月5日　椿耕太郎

二相状態での平均密度

関連する記事