


Next: 3.6 局所熱力学的平衡
Up: 3. 状態量(熱力学関数)
Previous: 3.4.2 ヘルムホルツの自由エネルギーとの関係
ピストンを動かさない体積が一定の状態で熱を加えると、加えた熱のエネルギー分だけ系の内部エネルギーが増える。しかし、系が体積一定ではなく、ピストンのような可動壁で周囲と隔てられている場合は、図3.5のように熱を加えると系は膨張しようとする。膨張での仕事の分、体積一定での変化よりも内部エネルギーの変化量は小さくなる。また熱を奪った場合、系は圧縮され周囲から仕事をされるため、内部エネルギーの減少量は小さくなる。可動壁を持つ系では、加えられた熱のエネルギー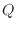 [J]の一部は必ず周囲に仕事
[J]の一部は必ず周囲に仕事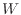 [J]として作用し内部エネルギーの増加量
[J]として作用し内部エネルギーの増加量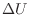 [J]との和が加えられた熱のエネルギーと等しい(式(1.7) p.
[J]との和が加えられた熱のエネルギーと等しい(式(1.7) p. ![[*]](crossref.png) )ことから次式のように表される。
)ことから次式のように表される。
このような可動壁で囲われた系では、エンタルピーを用いると計算が便利である。圧力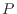 [Pa]の等圧環境では系の体積変化
[Pa]の等圧環境では系の体積変化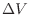 [m
[m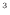 ]により、仕事
]により、仕事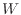 [J]は次式で表される。仕事は系がされるのが正、体積変化では仕事をされる圧縮が負としているので、符号は逆となる。
[J]は次式で表される。仕事は系がされるのが正、体積変化では仕事をされる圧縮が負としているので、符号は逆となる。
上2式から等圧環境で可動壁を持つ系に熱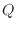 [J]を与えた場合の変化は次式で表される。
[J]を与えた場合の変化は次式で表される。
ここでエンタルピー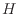 [J]を
[J]を
とすると、変化量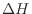 [J]は次のようになる。等圧変化であれば、
[J]は次のようになる。等圧変化であれば、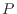 [Pa]は
[Pa]は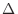 から外すことができる。
から外すことができる。
上式を式(3.7)へ代入すると、大気圧で可動壁に囲まれた系のような等圧過程に必要な熱は次式のようにエンタルピーの差のみで表すことが出来る。
大気中で可動壁を持つある系を、状態1から状態2へ変化させたいときに、必要な加熱量をエンタルピーを用いることで上式より簡単に求めることができる。また、可動壁を持つ系の中で燃焼のような発熱が起こるとき、圧力ごとのエンタルピーの変化量が分かっていれば、得られる熱量を簡単に知ることができる。



Next: 3.6 局所熱力学的平衡
Up: 3. 状態量(熱力学関数)
Previous: 3.4.2 ヘルムホルツの自由エネルギーとの関係
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![[*]](crossref.png) )ことから次式のように表される。
)ことから次式のように表される。
![]() [Pa]の等圧環境では系の体積変化
[Pa]の等圧環境では系の体積変化![]() [m
[m![]() ]により、仕事
]により、仕事![]() [J]は次式で表される。仕事は系がされるのが正、体積変化では仕事をされる圧縮が負としているので、符号は逆となる。
[J]は次式で表される。仕事は系がされるのが正、体積変化では仕事をされる圧縮が負としているので、符号は逆となる。