


Next: B.2 自由膨張過程
Up: B. サイクルと準静的過程
Previous: B. サイクルと準静的過程
B.1 サイクルでの仕事
熱機関のように系(ピストンを可動壁とする閉じた系を考える)から仕事を取り出したいサイクルにおいて、系の周囲の圧力を考えると、その周囲の圧力によりピストンの支持棒の力の向きが変化することがある。
系からピストンにかかる力と、周囲からピストンへかかる力と支持棒の力の和は釣り合う(図B.1)。系の圧力によりピストンに働く力は、ピストンへの系の圧力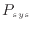 [Pa]とピストンの断面積
[Pa]とピストンの断面積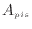 [m
[m ]で
]で
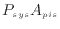 [N]と表される。周囲からピストンへの力は、周囲の圧力
[N]と表される。周囲からピストンへの力は、周囲の圧力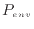 [Pa]、ピストンの断面積
[Pa]、ピストンの断面積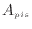 [m
[m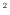 ]、ピストンの支持棒の力
]、ピストンの支持棒の力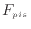 [N]で
[N]で
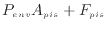 [N]と表される。この力の釣り合いから次式が成り立つ。
[N]と表される。この力の釣り合いから次式が成り立つ。
例えば車のエンジンのピストンなどは大気中で動作するため、周囲の空気にも仕事をしている。ピストンの周囲の圧力が大気圧の0.1 MPa(
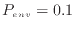 MPa
MPa 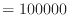 Pa)、ピストンの断面が0.1 m四方の正方形(
Pa)、ピストンの断面が0.1 m四方の正方形(
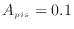 m
m
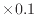 m
m 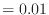 m
m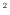 )を考える。この時、ピストンが周囲から内部に向かって、周囲の圧力により加えられる力は次のように計算できる。
)を考える。この時、ピストンが周囲から内部に向かって、周囲の圧力により加えられる力は次のように計算できる。
このとき、ピストン内部の圧力が10.0 MPa(
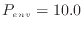 MPa
MPa
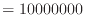 Pa)であると、系からピストンへ加えられる力は次のように計算できる。
Pa)であると、系からピストンへ加えられる力は次のように計算できる。
上の2つの値を式(B.1)へ代入すると、次のようにピストンで力が釣り合うために支持棒に加える必要のある力が求まる。
支持棒が99kNの力でピストンを押すと釣り合う。この釣り合っているピストンの支持棒の力をわずかに小さくすると、系は膨張する。簡単のため、系の体積が変化しても圧力は大きく変わらず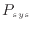 [Pa]は一定とし、体積が
[Pa]は一定とし、体積が
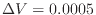 m
m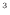 変化した場合を考える。このとき、ピストンの移動距離
変化した場合を考える。このとき、ピストンの移動距離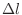 [m]は次のように計算される。
[m]は次のように計算される。
この際の、系がした仕事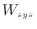 、系が周囲にした仕事
、系が周囲にした仕事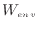 [J]、系が支持棒にした仕事
[J]、系が支持棒にした仕事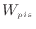 [J]の関係は次のようになる。この節でのみ仕事の符号の向きの定義を変え、系からも周囲からもピストンへ向かい方向の仕事を正とする。
[J]の関係は次のようになる。この節でのみ仕事の符号の向きの定義を変え、系からも周囲からもピストンへ向かい方向の仕事を正とする。
また、それぞれの値は次のように求められる。
系は5000 Jの仕事をしている。そのうち支持棒に4950 J、周囲に50 Jの仕事をしている。支持棒にされる仕事4950 Jがとり出される仕事、車のエンジンであれば車の動力である。
では、図B.2系の圧力が周囲の圧力よりも小さい場合はどうなるだろうか。例えば注射器を大気圧下で引く場合は注射器の内部の圧力が低い。ピストン(注射器)の周囲が同様に大気圧0.1 MPaで、系の圧力がそれよりも低い0.05 MPaのときを考える。ピストンの形状は同様とする。周囲の圧力により加えられる力は同様に
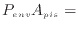 1 kNである。系からピストンへ加えられる力は次のように計算できる。
1 kNである。系からピストンへ加えられる力は次のように計算できる。
上の2つの値を式(B.1)へ代入すると、次のようにピストンで力が釣り合うために支持棒に加える必要のある力が求まる。
ピストンへ向かう方向が正であるので、支持棒はピストンを0.5 kNの力で引っ張っている。この際の、系がした仕事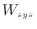 [J]、系が周囲にした仕事
[J]、系が周囲にした仕事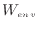 [J]、系が支持棒にした仕事
[J]、系が支持棒にした仕事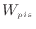 [J]は次のようになる。
[J]は次のようになる。
系は25 Jの仕事をしている。そのうち支持棒に-25 J、周囲に50 Jの仕事をしている。系と支持棒で25 Jずつ周囲に仕事をしていることになる。
このように、周囲の圧力が系の圧力よりも高い場合には、系が膨張する場合にもピストンの支持棒を引っ張る必要があり、系が仕事をされているように感じるが、系とピストンはともに周囲に仕事をしている。
ここで仕事はすべて正の値とすると、以下の関係が成り立つ。
“系が大気にする仕事”が“系がする仕事”よりも大きい場合、系が膨張する場合でも注射器を引っ張るように引っ張って仕事をする必要があり、“取り出せる仕事”が負の値となる。通常、“系が周囲にする仕事”はピストンが周囲の圧力にする仕事のみではなく、支持棒への仕事を含めた、系がピストンにする仕事を考える。



Next: B.2 自由膨張過程
Up: B. サイクルと準静的過程
Previous: B. サイクルと準静的過程
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() MPa
MPa ![]() Pa)、ピストンの断面が0.1 m四方の正方形(
Pa)、ピストンの断面が0.1 m四方の正方形(
![]() m
m
![]() m
m ![]() m
m![]() )を考える。この時、ピストンが周囲から内部に向かって、周囲の圧力により加えられる力は次のように計算できる。
)を考える。この時、ピストンが周囲から内部に向かって、周囲の圧力により加えられる力は次のように計算できる。
![]() 1 kNである。系からピストンへ加えられる力は次のように計算できる。
1 kNである。系からピストンへ加えられる力は次のように計算できる。