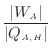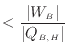


Next: B. 閉じた系のサイクルでの過程
Up: A. 熱力学第二法則と不可逆性
Previous: A.3 熱力学第二法則のトムソンの原理とクラウジウスの原理
A.4 可逆サイクルの効率
可逆サイクルの熱機関としての性能が不可逆サイクルの熱機関の性能よりも低いと熱力学第二法則に反することを1.4.5節
 に示した。
不可逆サイクル熱機関Aと可逆サイクル熱機関Bを考える。ここで、不可逆の熱機関Aの効率
に示した。
不可逆サイクル熱機関Aと可逆サイクル熱機関Bを考える。ここで、不可逆の熱機関Aの効率
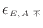 [-]が可逆サイクル熱機関Bの効率
[-]が可逆サイクル熱機関Bの効率
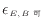 [-]よりも低い場合には熱力学第二法則に反しないことを示す(図A.5)。
[-]よりも低い場合には熱力学第二法則に反しないことを示す(図A.5)。
式(1.12)
 より次式が成り立つ。
より次式が成り立つ。
不可逆の熱機関Aは逆にヒートポンプとして動作させることはできない。可逆の熱機関Bは可逆であるのでヒートポンプとしても動作できる(図A.5-2)ので、不可逆の熱機関Aと同じ大きさの仕事で(
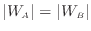 )ヒートポンプとして動作させる(図A.5-3)と次式が成り立つ。
)ヒートポンプとして動作させる(図A.5-3)と次式が成り立つ。
全体として高温熱源から低温熱源に熱が伝わっている(図A.5-4)ので、熱力学第二法則に反しない。



Next: B. 閉じた系のサイクルでの過程
Up: A. 熱力学第二法則と不可逆性
Previous: A.3 熱力学第二法則のトムソンの原理とクラウジウスの原理
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。