準静的過程でない過程が不可逆過程となる場合には、周囲と系との間で熱力学的平衡が成り立たない場合と、系の内部で熱力学的平衡が成り立たない場合がある。どちらの場合でも、平衡が成り立たない過程では過程中の損失により不可逆になる。周囲と系の熱力学的平衡について、ここでは閉じた系を考え相平衡と化学平衡は考えない。そこで、周囲と系との力学平衡と熱平衡が成り立たない条件を考える。
外部と仕事のやり取りのあるサイクルでは必ずピストンのような可動部が存在する。力学平衡が成り立たない場合には、このピストンを挟んで周囲と系の圧力が異なる。この原因として、ピストンが動く際のピストンと容器との間で働く摩擦力と、ピストンを動かすために必要な慣性力に対する力が考えられる。
質量
[kg]のピストンの速度
[m/s]を変化させる（停止の速度ゼロから増やす）には、慣性力に対して次式で表される力
[N]が必要である。
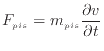
ピストンの面積が
[m
]であれば、系の圧力
[Pa]と周囲の圧力
[Pa]の差により表される。
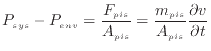
上式で表される圧力差がないとピストンは動き出さない（膨張では
、圧縮では
）。
また、ピストンが動く際にピストンを支えている壁との間に必ず摩擦が生じ摩擦力が動きと逆方向に働く。摩擦力などの力が働いている際には周囲と系と間に圧力差がある。摩擦力は有限の大きさであるので、微小な圧力差
[Pa]では摩擦力に対抗しピストンを動かすことはできない。そのため、準静的過程では質量がなく摩擦のない理想的なピストンを考えなくてはいけない。
また、ピストンの移動速度によりやりとりする仕事が変化することも考えられる
B.2。
系の内部での平衡の条件を考える。過程において系の内部で力学平衡となっていない条件として、内部で圧力分布があり流れが起きる状態があげられる。 力学平衡が成り立たない条件では熱平衡も成り立たない。ピストンに摩擦力が働くと容器との間に摩擦熱が発生する（周囲とやり取りされる仕事の一部が摩擦熱に変換されているため、エネルギーは保存されている）。また、ピストンを押した場合にピストンの運動エネルギーが流体に伝わり内部で流れが発生し、流れが徐々に小さな渦となることにより流体の運動エネルギーが熱に変換されることでも熱平衡が成り立たなくなる（粘性消散）。熱に変換される（発熱する）ことにより、ある場所での温度が高くなり熱平衡ではなくなる。 また、内部の熱平衡が成り立たなければ、力学平衡も成り立たない。熱平衡が成り立っていなければ熱が伝わり温度が変化する。温度が変われば圧力も変化するため力学平衡が崩れる。
また、熱が移動するには温度差が必要であり、必ず熱平衡状態とはならない。固体壁を挟んだ熱の移動
[J]は熱伝導で伝わり、熱伝導の式（フーリエの法則）により次のようになる（壁の中の温度分布は線形と仮定する）B.3。
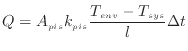
ここで
![$ k_{pis} \left[ \dfrac{\rm W}{\rm K \cdot m} \right]$](img523.png)
はピストンの壁の熱伝導率、
[℃]は壁の周囲側の温度、
[℃]は壁の内部側の温度、
[m]はピストンの壁の厚さ、
[s]は熱が伝わっている時間である。実際の現象では、熱は温度の高いところから低いところへ伝わり不可逆である。熱は熱平衡状態では伝わらない。
内部が熱平衡でない場合には熱平衡の場合に比べ、膨張過程で取り出せる仕事が小さくなり、圧縮過程で必要な仕事が大きくなる。例えば、等温変化において圧力変化での圧縮や膨張による内部の温度変化が、壁からの伝熱による温度変化よりも早ければ、内部の温度が周囲の等温環境の温度とは異なる。膨張過程では周囲よりも温度が低くなり、周囲と同じ温度の場合よりも圧力が低くなる。そのため取り出せる仕事は小さくなる。圧縮過程では周囲よりも温度が高くなり、周囲と同じ温度の場合よりも圧力が高くなる。そのため必要な仕事が大きくなる。
不可逆過程ではサイクル内部の流体が可逆過程と同じ仕事のやりとりをしても、外部とやり取りする仕事の大きさが異なる。不可逆損失の多くがピストンの可動壁によるものであり、ピストンの可動壁がなく、系内で局所熱力学的平衡（4.4節
）が成り立っており十分に小さな系を考えれば、実際の現象においても断熱変化は可逆過程となりうる（系の内部で流れによる粘性消散B.4がある場合は不可逆）。