


Next: B.5 不可逆過程での不可逆損失
Up: B. 閉じた系のサイクルでの過程
Previous: B.3 なにも起こらないサイクル
B.4 準静的過程における微小差
準静的過程において、系と周囲は熱平衡と力学平衡が成り立っており、系と周囲の温度と圧力は等しい。しかし、熱や仕事のやり取りをするには温度差や圧力差が必要である。準静的過程においては、ゼロの極限をとった微小な差をとり、無限の時間をかけることにより熱や仕事のやり取りをする。この状態で、系と周囲の温度や圧力は等しいのだろうか、異なっているのだろうか。準静的過程とは、平衡を維持したまま変化する過程であるので、温度と圧力は等しくなくてはいけない。
この準静的過程でのゼロの極限をとった微小な差について考えよう。ゼロの極限をとった微小な温度差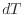 [℃]は次のように表される。
[℃]は次のように表される。
ここで、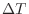 [℃]は任意の有限の温度差とする。例として壁での熱伝導による熱の伝わりを考えると、熱伝導の式(フーリエの法則B.1)により次のようになる(壁の中の温度分布は線形と仮定する)。
[℃]は任意の有限の温度差とする。例として壁での熱伝導による熱の伝わりを考えると、熱伝導の式(フーリエの法則B.1)により次のようになる(壁の中の温度分布は線形と仮定する)。
ここで、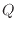 [J]は伝わる熱量、
[J]は伝わる熱量、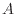 [m
[m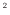 ]は熱の伝わる面積、
]は熱の伝わる面積、
![$ k \left [\dfrac{\rm W}{\rm K \cdot m} \right ]$](img510.png) は壁の熱伝導率、
は壁の熱伝導率、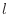 [m]は壁の厚さ、
[m]は壁の厚さ、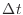 [s]は経過時間である。ここで、温度差
[s]は経過時間である。ここで、温度差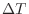 [℃]に微小な温度差
[℃]に微小な温度差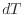 [℃]を代入する。
[℃]を代入する。
面積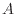 [m
[m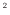 ]、熱伝導率
]、熱伝導率
![$ k \left [\dfrac{\rm W}{\rm K \cdot m} \right ]$](img510.png) は有限の大きさであり、経過時間
は有限の大きさであり、経過時間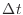 [s]もどれだけ大きな時間(例えば1億年)経過しても有限の大きさである限り
[s]もどれだけ大きな時間(例えば1億年)経過しても有限の大きさである限り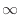 で割ればゼロとなる。このように、どれだけ長くても有限の時間の経過であれば、ゼロの極限をとった差はゼロとみなせ、系と周囲の温度が等しいと考えられる。経過時間
で割ればゼロとなる。このように、どれだけ長くても有限の時間の経過であれば、ゼロの極限をとった差はゼロとみなせ、系と周囲の温度が等しいと考えられる。経過時間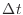 [s]が
[s]が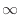 である場合のみ分母の
である場合のみ分母の を消すとことができるため、無限の経過時間でのみゼロの極限をとった差により熱を伝えることができる。
を消すとことができるため、無限の経過時間でのみゼロの極限をとった差により熱を伝えることができる。



Next: B.5 不可逆過程での不可逆損失
Up: B. 閉じた系のサイクルでの過程
Previous: B.3 なにも起こらないサイクル
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() [℃]は次のように表される。
[℃]は次のように表される。
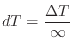
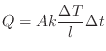
![$ k \left [\dfrac{\rm W}{\rm K \cdot m} \right ]$](img510.png) は壁の熱伝導率、
は壁の熱伝導率、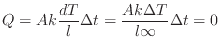
![$ k \left [\dfrac{\rm W}{\rm K \cdot m} \right ]$](img510.png) は有限の大きさであり、経過時間
は有限の大きさであり、経過時間