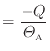
熱が与えられる物体Bでは次式となる。
全体のエントロピーの変化
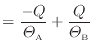
ここで準静等温過程では熱が伝わる物体間には温度差がないので
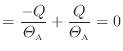
以上のように、可逆過程である準静等温過程では全体のエントロピーは変化しない。
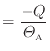
熱が与えられる物体Bでは次式となる。
全体のエントロピーの変化
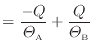
ここで、熱は温度の高い物体から低い物体に伝わるので
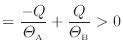
以上のように、通常の熱が伝わる不可逆過程では全体のエントロピーは増加する。
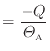
熱が与えられる物体Bでは次式となる。
全体のエントロピーの変化
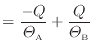
ここで準静等温過程では熱が伝わる物体間には温度差がないので
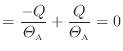
以上のように、可逆過程である準静等温過程では全体のエントロピーは変化しない。
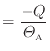
熱が与えられる物体Bでは次式となる。
全体のエントロピーの変化
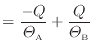
ここで、熱は温度の高い物体から低い物体に伝わるので
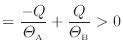
以上のように、通常の熱が伝わる不可逆過程では全体のエントロピーは増加する。