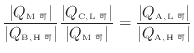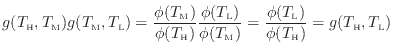


Next: 1.4.7 可逆熱機関(可逆ヒートポンプ)と温度
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.5 可逆と不可逆の熱機関(ヒートポンプ)での効率の比較
熱源の条件である温度と可逆熱機関(可逆ヒートポンプ)の効率の関係を明らかにする。同じ組み合わせの一定温度の熱源二つで動作する可逆熱機関(可逆ヒートポンプ)は、どんな熱機関やヒートポンプでも必ず同じ効率となり構成によらない(1.4.4節
 )。では、同じ組み合わせの熱源でなく異なる組み合わせの熱源で動作する可逆熱機関(可逆ヒートポンプ)での効率ではどうなるだろうか。一定温度の熱源二つの組み合わせが決まれば効率は可逆熱機関(可逆ヒートポンプ)の構成にはよらないので、効率を決める要素は二つの熱源の条件だけである。熱源と系は熱のやり取りしかしなく熱のやり取りに影響するのは温度のみであるので、可逆熱機関(可逆ヒートポンプ)の効率を決める条件は二つの熱源の一定の温度の組み合わせのみである。よって温度
)。では、同じ組み合わせの熱源でなく異なる組み合わせの熱源で動作する可逆熱機関(可逆ヒートポンプ)での効率ではどうなるだろうか。一定温度の熱源二つの組み合わせが決まれば効率は可逆熱機関(可逆ヒートポンプ)の構成にはよらないので、効率を決める要素は二つの熱源の条件だけである。熱源と系は熱のやり取りしかしなく熱のやり取りに影響するのは温度のみであるので、可逆熱機関(可逆ヒートポンプ)の効率を決める条件は二つの熱源の一定の温度の組み合わせのみである。よって温度
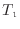 [℃またはK]の熱源1と温度
[℃またはK]の熱源1と温度
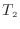 [℃またはK]の熱源2(
[℃またはK]の熱源2(
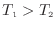 )で動作する可逆熱機関(可逆ヒートポンプ)の効率は二つの熱源の温度(
)で動作する可逆熱機関(可逆ヒートポンプ)の効率は二つの熱源の温度(
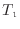 [℃またはK]、
[℃またはK]、
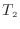 [℃またはK])の関数となる1.17。
[℃またはK])の関数となる1.17。
この効率を表す関数
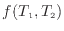 がどのような関数か明らかにするため、図1.10に示すように、温度
がどのような関数か明らかにするため、図1.10に示すように、温度
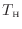 [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
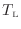 [℃またはK]の熱源で動作する可逆熱機関Aと、温度
[℃またはK]の熱源で動作する可逆熱機関Aと、温度
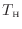 [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
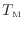 [℃またはK]の熱源で動作する可逆熱機関B、温度
[℃またはK]の熱源で動作する可逆熱機関B、温度
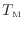 [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
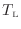 [℃またはK]の熱源で動作する可逆熱機関Cを考える。このとき熱源の温度の関係は
[℃またはK]の熱源で動作する可逆熱機関Cを考える。このとき熱源の温度の関係は
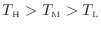 とする。
とする。
この場合の各可逆熱機関の効率は可逆熱機関の効率の式(1.13)
 と式(1.22)から熱源の温度により次のように表される。
と式(1.22)から熱源の温度により次のように表される。
ここで熱力学第一法則、式(1.12)
 より
より
が成り立つ。熱源と可逆熱機関のやりとりは熱であるので、やりとりする熱と熱源の条件である温度との関係とするために、上3式を左辺の高温側熱源から伝わる熱量で割り、それぞれの効率(式(1.23)-式(1.25))を代入し変形する。それぞれ以下の熱源と可逆熱機関がやりとりする熱量と熱源の温度の関係が成り立つ。
ここで上3式の最右辺は二つの熱源の温度のみの関数である。そこで、簡単に書き表すために次式のような関数
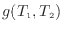 をおく。
をおく。
式(1.26)-式(1.28)へ式(1.29)を適用すると、それぞれの可逆熱機関での高温熱源からの熱と低温熱源からの熱の大きさの比は次のように温度の関数で表される。
温度の関数
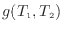 を明らかにするため、それぞれの可逆熱機関と熱源との熱の大きさの関係を用いる。可逆熱機関Bの低温側の熱源へ伝わる熱の大きさ
を明らかにするため、それぞれの可逆熱機関と熱源との熱の大きさの関係を用いる。可逆熱機関Bの低温側の熱源へ伝わる熱の大きさ
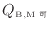 [J]と、可逆熱機関Cの高温側の熱源から伝わる熱の大きさ
[J]と、可逆熱機関Cの高温側の熱源から伝わる熱の大きさ
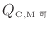 [J]を、同じ大きさ
[J]を、同じ大きさ
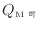 [J]になるよう
1.18にそれぞれの可逆熱機関を動作させて(
[J]になるよう
1.18にそれぞれの可逆熱機関を動作させて(
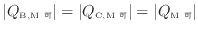 )、可逆熱機関Bと可逆熱機関Cを一つの可逆熱機関として動作させる。可逆熱機関Bと可逆熱機関Cの熱量の比の積から、次式の関係が成り立つ。
)、可逆熱機関Bと可逆熱機関Cを一つの可逆熱機関として動作させる。可逆熱機関Bと可逆熱機関Cの熱量の比の積から、次式の関係が成り立つ。
次に可逆熱機関の効率の関係から別の熱の式を求める。可逆熱機関Bと可逆熱機関Cを合わせた一つの可逆熱機関として考えると、温度
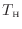 [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
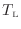 [℃またはK]の同じ二つの熱源の間で動作する可逆熱機関とみなせるので、可逆熱機関Aと効率は等しくなる。効率が等しいので伝わる熱の大きさの比は可逆熱機関Aと等しく次式が成り立つ。
[℃またはK]の同じ二つの熱源の間で動作する可逆熱機関とみなせるので、可逆熱機関Aと効率は等しくなる。効率が等しいので伝わる熱の大きさの比は可逆熱機関Aと等しく次式が成り立つ。
二つの熱の式である式(1.33)と式(1.34)から次の関係が成り立つ。
熱の関係式である上式に式(1.30)、式(1.31)、式(1.32)を代入すると温度の関係式が関数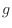 で次のように表す事ができる1.19。
で次のように表す事ができる1.19。
この式から関数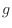 がどのような関数かを考える。ここで、左辺は
がどのような関数かを考える。ここで、左辺は
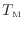 [℃またはK]を含む関数となっているが、右辺は
[℃またはK]を含む関数となっているが、右辺は
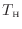 [℃またはK]と
[℃またはK]と
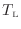 [℃またはK]のみの関数で
[℃またはK]のみの関数で
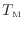 [℃またはK]の関数ではない。そのため、関数
[℃またはK]の関数ではない。そのため、関数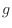 は左辺で
は左辺で
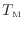 [℃またはK]が消える形の関数である必要がある。積で
[℃またはK]が消える形の関数である必要がある。積で
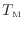 [℃またはK]が消えるように関数
[℃またはK]が消えるように関数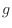 を、ある温度の関数
を、ある温度の関数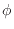 (ファイ)で以下の形で表す。
(ファイ)で以下の形で表す。
上式のように関数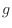 が温度の商の関数だと、次式のように
が温度の商の関数だと、次式のように
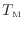 [℃またはK]が左辺から消える。
[℃またはK]が左辺から消える。
このように関数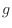 が温度の商の関数であることが分かった。熱源の温度と、熱源とやりとりする熱量の関係をまとめると式(1.29)と式(1.35)より次式が成り立つ。
が温度の商の関数であることが分かった。熱源の温度と、熱源とやりとりする熱量の関係をまとめると式(1.29)と式(1.35)より次式が成り立つ。



Next: 1.4.7 可逆熱機関(可逆ヒートポンプ)と温度
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.5 可逆と不可逆の熱機関(ヒートポンプ)での効率の比較
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。
![]() がどのような関数か明らかにするため、図1.10に示すように、温度
がどのような関数か明らかにするため、図1.10に示すように、温度
![]() [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
![]() [℃またはK]の熱源で動作する可逆熱機関Aと、温度
[℃またはK]の熱源で動作する可逆熱機関Aと、温度
![]() [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
![]() [℃またはK]の熱源で動作する可逆熱機関B、温度
[℃またはK]の熱源で動作する可逆熱機関B、温度
![]() [℃またはK]の熱源と温度
[℃またはK]の熱源と温度
![]() [℃またはK]の熱源で動作する可逆熱機関Cを考える。このとき熱源の温度の関係は
[℃またはK]の熱源で動作する可逆熱機関Cを考える。このとき熱源の温度の関係は
![]() とする。
とする。
![]() と式(1.22)から熱源の温度により次のように表される。
と式(1.22)から熱源の温度により次のように表される。
![]() を明らかにするため、それぞれの可逆熱機関と熱源との熱の大きさの関係を用いる。可逆熱機関Bの低温側の熱源へ伝わる熱の大きさ
を明らかにするため、それぞれの可逆熱機関と熱源との熱の大きさの関係を用いる。可逆熱機関Bの低温側の熱源へ伝わる熱の大きさ
![]() [J]と、可逆熱機関Cの高温側の熱源から伝わる熱の大きさ
[J]と、可逆熱機関Cの高温側の熱源から伝わる熱の大きさ
![]() [J]を、同じ大きさ
[J]を、同じ大きさ
![]() [J]になるよう
1.18にそれぞれの可逆熱機関を動作させて(
[J]になるよう
1.18にそれぞれの可逆熱機関を動作させて(
![]() )、可逆熱機関Bと可逆熱機関Cを一つの可逆熱機関として動作させる。可逆熱機関Bと可逆熱機関Cの熱量の比の積から、次式の関係が成り立つ。
)、可逆熱機関Bと可逆熱機関Cを一つの可逆熱機関として動作させる。可逆熱機関Bと可逆熱機関Cの熱量の比の積から、次式の関係が成り立つ。