


Next: 3.1.6 ヒートポンプ
Up: 3.1 閉じた系のサイクル
Previous: 3.1.4.1 問題
3.1.5 熱機関
二つの熱源間で動作する閉じた系の熱機関のわかりやすい例として、一つの過程で熱か仕事どちらかだけのやりとりとなる過程で構成されたサイクルを考える。系の体積を変化させず仕事のやりとりなしで外部と熱のみのやりとりをする等積加熱・冷却過程と、系と外部で熱のやりとりをせず体積を変化させ外部と仕事のみのやりとりをする断熱膨張・圧縮過程による熱機関を考える。先を塞いだ注射器やピストンをイメージして、図3.6のようなサイクルを考えよう。図3.6の状態1からピストンを動かないように固定し、低温の熱源の中に入れる(例えば冷たい水の中)。ピストンから冷たい水に熱が伝わり、等積冷却過程でピストン内部の温度が下がる(状態2)。冷たい水からピストンを取り出し熱が伝わらないようにして、ピストンをさらに押し断熱圧縮過程で体積を小さくする(状態3)。次はピストンを固定し温かいお湯の中にピストンを入れ等積加熱過程で変化させる(状態4)。お湯からピストンを取り出し、元の状態に戻るまで断熱膨張過程でピストンを膨張させる(状態1)。元の状態に戻り一連の過程がサイクルとなる。
図 3.6:
ピストンでの熱機関として動作するサイクル
|
|
サイクルでは周囲と熱と仕事をやりとりする。それぞれの過程では以下のことが起こっている。
- 1→2 冷却され熱が周囲に伝わる(等積冷却過程) → 内部の圧力が低下
- 2→3 圧縮され周囲から仕事をされる(断熱圧縮過程) → 体積が減少
- 3→4 加熱され熱が周囲から伝わる(等積加熱過程) → 内部の圧力が上昇
- 4→1 膨張し周囲に仕事をする(断熱膨張過程) → 体積が増加
冷却(1→2)や加熱(3→4)をされると、圧力が変化し、断熱変化(2→3、4→1)で体積が変化することにより周囲と仕事のやりとりをする。圧力の変化の概略は図3.7のようになる(圧力変化の傾きは例として示したもので、過程によって異なることもある)。図3.8に温度変化の概略を示す(温度変化の傾きは例として示したものである)。断熱圧縮過程(2→3)では温度は上昇し、断熱膨張過程(4→1)では温度は低下する。体積増加の際の仕事については付録B.1
 に詳細を記した。
に詳細を記した。
図 3.7:
ピストンでの熱機関として動作するサイクルの圧力変化
|
|
外部からサイクルに仕事をしている2→3の過程での仕事
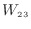 [J]と外部へサイクルが仕事をしている4→1の過程での仕事
[J]と外部へサイクルが仕事をしている4→1の過程での仕事
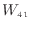 [J]の関係は、熱機関として外部へ仕事を取り出すために
[J]の関係は、熱機関として外部へ仕事を取り出すために
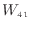 [J]が大きい必要がある。式(3.4)
[J]が大きい必要がある。式(3.4)
 より、仕事
より、仕事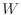 [J]は圧力
[J]は圧力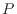 [Pa]と微小体積変化
[Pa]と微小体積変化
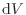 [m
[m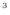 ]の積分により
]の積分により
で表される。
状態2から状態3と状態4から状態1での体積の変化量は同じであるので、どちらの仕事が大きいかは過程中の圧力によって決まる。図3.7から、状態2から状態3の平均圧力より、状態4から状態1の平均圧力が大きいことが分かる。そのため、積分して得られる仕事も大きくなり、以下の式が得られる。
過程2→3では仕事
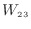 をされるため正の値、過程4→1では仕事
をされるため正の値、過程4→1では仕事
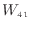 をするため負の値となることを考慮し、上式の絶対値記号を外し次式が得られる。
をするため負の値となることを考慮し、上式の絶対値記号を外し次式が得られる。
状態2から状態3では周囲から仕事をされ、状態4から状態1では周囲に仕事をしている。このサイクルでは
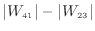 [J]の仕事を周囲にしている3.8。また、サイクルが受け取る熱とサイクルが周囲に与える熱の大きさを比較する。状態3から状態4で周囲(高温の熱源3-4)から熱を受け取り、状態1から状態2で周囲(低温の熱源1-2)に熱を与えている。図3.8の温度変化の概略に示すように、周囲の温度は状態3から状態4の熱源3-4が状態1から状態2の熱源1-2よりも高い。このことから、このサイクルは高温の熱源3-4から熱を受け取り、低温の熱源1-2へ熱を与えている。
[J]の仕事を周囲にしている3.8。また、サイクルが受け取る熱とサイクルが周囲に与える熱の大きさを比較する。状態3から状態4で周囲(高温の熱源3-4)から熱を受け取り、状態1から状態2で周囲(低温の熱源1-2)に熱を与えている。図3.8の温度変化の概略に示すように、周囲の温度は状態3から状態4の熱源3-4が状態1から状態2の熱源1-2よりも高い。このことから、このサイクルは高温の熱源3-4から熱を受け取り、低温の熱源1-2へ熱を与えている。
図 3.8:
ピストンでの熱機関として動作するサイクルの温度変化
|
|
状態1から再度状態1へ戻るとき、内部エネルギーの値は等しく変化はゼロであるので、エネルギー保存の式(1.5)
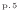 から以下の式が成り立つ。
から以下の式が成り立つ。
仕事の大きさの関係の式(3.6)
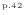 と上式から、熱の大きさの関係を求めると以下の式が成り立つ。
と上式から、熱の大きさの関係を求めると以下の式が成り立つ。
過程1→2では熱
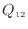 が外部に伝わるため負の値となり、過程3→4では外部から熱
が外部に伝わるため負の値となり、過程3→4では外部から熱
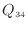 を受け取り正の値となることを考慮し絶対値をとり次式を得る。
を受け取り正の値となることを考慮し絶対値をとり次式を得る。
上式のように低温熱源へ渡す熱の大きさよりも、高温熱源から受け取る熱の大きさのほうが大きい。以上から、高温熱源から熱
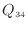 [J]を受け取り、一部を仕事
[J]を受け取り、一部を仕事
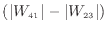 [J]に変換し外部へ取り出し、高温熱源から受け取った熱より少ない残りの熱
[J]に変換し外部へ取り出し、高温熱源から受け取った熱より少ない残りの熱
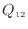 [J]を低温熱源へ渡している、すなわち熱機関として動作していることがわかる。
[J]を低温熱源へ渡している、すなわち熱機関として動作していることがわかる。
このように高温と低温の二つの熱源で動作する熱機関を1章では図3.9のように○で表していた。仕事は周囲にした仕事と周囲からされた仕事の差
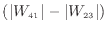 [J]をまとめて示した。図3.9では左の特定の四過程からなるサイクルと対応させているが、○で表した際には熱機関であることだけを表しどのような過程で構成された熱機関でもよい。
[J]をまとめて示した。図3.9では左の特定の四過程からなるサイクルと対応させているが、○で表した際には熱機関であることだけを表しどのような過程で構成された熱機関でもよい。
図3.6で例として示したサイクルはオットーサイクルと呼ばれ、ガソリンエンジンの理論サイクルである。このサイクルの各過程をガソリンエンジンと対応させると次のようになる(図3.10)。
- 1→2 冷却され熱が周囲に伝わる(等積冷却過程) → 燃焼後のガソリンと空気の混合気体を捨てて新しい空気を取り込む。排気して吸気をするとピストンが同じ位置に戻るので、これで等積の一過程とする
- 2→3 圧縮され周囲から仕事をされる(断熱圧縮過程) → 他のピストンから仕事をされ空気が圧縮される
- 3→4 加熱され熱が周囲から伝わる(等積加熱過程) → ガソリンと空気の混合気体に点火し瞬間的に燃焼させる。燃焼時間は一瞬であるため膨張による体積変化はほとんどなく、燃焼熱により加熱されるので、等積加熱となる
- 4→1 膨張し周囲に仕事をする(断熱膨張過程) → 前過程で圧力が上がっているので、膨張することで周囲に仕事をする
ガソリンエンジンでは作動流体が熱源となる。低温側では低温熱源となる大気を直接サイクルに取り込み、高温側では作動流体を直接燃焼させることで高温熱源とする。作動流体が熱源となるので、熱源と作動流体で熱交換をする必要がない3.9。ガソリンエンジンのように作動流体が熱源となるサイクルでは熱交換により作動流体の温度差が小さくなることがないためサイクルの効率が高くなる。効率は30〜40%程度である[#!1990Imajo!#][#!2011Nikkei!#][#!WebToyota!#]。
エンジンの他に実際に世の中で使われている熱機関として閉じた系のサイクルではないが火力発電所や原子力発電所がある。発電所の蒸気タービンを用いた汽力発電は系の中の物質に水を用いている。発電所と図3.6
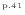 のサイクルの対応は以下のようになっている。
のサイクルの対応は以下のようになっている。
- 1→2 冷却され熱が周囲に伝わる : 復水器(海水で冷却)
- 2→3 圧縮され周囲から仕事をされる : ポンプ(水を循環させる)
- 3→4 加熱され熱が周囲から伝わる : ボイラー(燃焼や核反応で水を沸騰させる)
- 4→1 膨張し周囲に仕事をする : 蒸気タービン(発電機へとつながっており電気を発生させる)
新しい火力発電所では、エンジンと同じく作動流体を直接熱源とするガスタービンと蒸気タービンを併用したコンバインドサイクルを用いて50〜60%と高効率な発電をしている[#!WebDenki!#][#!WebToden!#]。



Next: 3.1.6 ヒートポンプ
Up: 3.1 閉じた系のサイクル
Previous: 3.1.4.1 問題
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。
![\includegraphics[width=50mm]{figures/ClosedCycleVolumeHeatengine.eps}](img326.png)
![]() に詳細を記した。
に詳細を記した。
![]() [J]と外部へサイクルが仕事をしている4→1の過程での仕事
[J]と外部へサイクルが仕事をしている4→1の過程での仕事
![]() [J]の関係は、熱機関として外部へ仕事を取り出すために
[J]の関係は、熱機関として外部へ仕事を取り出すために
![]() [J]が大きい必要がある。式(3.4)
[J]が大きい必要がある。式(3.4)
![]() より、仕事
より、仕事![]() [J]は圧力
[J]は圧力![]() [Pa]と微小体積変化
[Pa]と微小体積変化
![]() [m
[m![]() ]の積分により
]の積分により
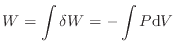
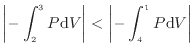
![]() から以下の式が成り立つ。
から以下の式が成り立つ。
![]() [J]をまとめて示した。図3.9では左の特定の四過程からなるサイクルと対応させているが、○で表した際には熱機関であることだけを表しどのような過程で構成された熱機関でもよい。
[J]をまとめて示した。図3.9では左の特定の四過程からなるサイクルと対応させているが、○で表した際には熱機関であることだけを表しどのような過程で構成された熱機関でもよい。
![]() のサイクルの対応は以下のようになっている。
のサイクルの対応は以下のようになっている。