


Next: 1.2.2 内部エネルギー
Up: 1.2 熱力学第一法則
Previous: 1.2 熱力学第一法則
1.2.1 仕事(力学的エネルギー)
力学で定義されるエネルギーである仕事について確認する。仕事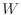 [J]は、力
[J]は、力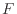 [N]を加えながら移動した距離
[N]を加えながら移動した距離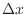 [m]により、次式の様に定義される。
[m]により、次式の様に定義される。
微小な移動距離
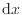 [m]での微小仕事
[m]での微小仕事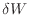 [J]は次のようになる
1.2。
[J]は次のようになる
1.2。
仕事は、ある物体から別の物体へ力が作用した際に伝わるエネルギーの形態であり、作用した後は力を加えられた物体の保有する位置エネルギーや運動エネルギー
1.3となる。バットでボールを打つ時を例に取る。ボールがバットに接触した位置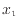 から、バットから離れる位置
から、バットから離れる位置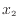 の間はバットからボールへ力
の間はバットからボールへ力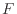 が加わっており
1.4は微小な仕事
が加わっており
1.4は微小な仕事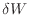 が連続して作用している。全体ではバットからボールへは次式で表される仕事
が連続して作用している。全体ではバットからボールへは次式で表される仕事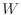 が作用する。
が作用する。
仕事が全てボールの保有する力学的エネルギー(運動エネルギー、位置エネルギー)に変換されたとする。仕事をされている間にボールの速度は上がり運動エネルギー
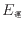 は高くなり、バットによって上もしくは下に叩かれていれば位置エネルギー
は高くなり、バットによって上もしくは下に叩かれていれば位置エネルギー
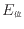 も同様に変化する。仕事の作用前を下付1、仕事の作用後を下付2で表せば力学的なエネルギーの保存から次の関係が成り立つ。
も同様に変化する。仕事の作用前を下付1、仕事の作用後を下付2で表せば力学的なエネルギーの保存から次の関係が成り立つ。
熱力学では作用するエネルギーに仕事だけでなく熱も考え、物体が保有するエネルギーに内部エネルギーが加わる。
系に仕事が作用する際の式(1.1)での
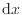 により、仕事を二通りに分けて考える。一つは系の境界に力が加わり系の形(体積)が変わったことにより
により、仕事を二通りに分けて考える。一つは系の境界に力が加わり系の形(体積)が変わったことにより
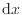 が生じる仕事であり、ピストン形状の系での体積変化が典型的である(図1.1(a))。もう一つは系の内部で系の一部に力が加わり
が生じる仕事であり、ピストン形状の系での体積変化が典型的である(図1.1(a))。もう一つは系の内部で系の一部に力が加わり
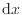 動くことによる仕事であり、例として系の内部にプロペラがあり系の外からプロペラの軸の回転で力を伝え仕事が作用するような系が挙げられる(図1.1(b))。
動くことによる仕事であり、例として系の内部にプロペラがあり系の外からプロペラの軸の回転で力を伝え仕事が作用するような系が挙げられる(図1.1(b))。



Next: 1.2.2 内部エネルギー
Up: 1.2 熱力学第一法則
Previous: 1.2 熱力学第一法則
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。
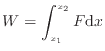
![]() により、仕事を二通りに分けて考える。一つは系の境界に力が加わり系の形(体積)が変わったことにより
により、仕事を二通りに分けて考える。一つは系の境界に力が加わり系の形(体積)が変わったことにより
![]() が生じる仕事であり、ピストン形状の系での体積変化が典型的である(図1.1(a))。もう一つは系の内部で系の一部に力が加わり
が生じる仕事であり、ピストン形状の系での体積変化が典型的である(図1.1(a))。もう一つは系の内部で系の一部に力が加わり
![]() 動くことによる仕事であり、例として系の内部にプロペラがあり系の外からプロペラの軸の回転で力を伝え仕事が作用するような系が挙げられる(図1.1(b))。
動くことによる仕事であり、例として系の内部にプロペラがあり系の外からプロペラの軸の回転で力を伝え仕事が作用するような系が挙げられる(図1.1(b))。