• 学問 -top-

3.2.1 準静的過程

可逆サイクルは可逆過程から成り立つ。しかし、熱が伝わる過程は必ず不可逆の過程となる（1.3.2節 $^{\text{p.\pageref{sec-HeatIrreversibility}}}$ ）。また、体積の変化する（ピストンの動く）過程では、ピストンを動かすために内部からと周囲からの力で動く方向の力が大きくならなくてはならないため、不可逆となる。そこで可逆の過程を考えるために、現実には実現不可能ではあるが無限の時間をかける準静的過程を考える。準静的過程では考えている閉じた系と周囲との間で常に平衡が成り立っており、系の内部と周囲でもそれぞれ平衡が維持されている過程である。平衡状態は釣り合いがとれ変化をしなくなった状態であるので、可逆の現象である。しかし、平衡状態が続いても状態は変化しない。そこで平衡状態で極微小な変化をしており、その変化が無限時間続くことで平衡状態で可逆の変化が起こる、と考えるのが準静的過程である。 3.1.1節 $^{\text{p.\pageref{sec-Equilibrium}}}$ で示した熱力学的平衡の熱平衡、力学平衡、相平衡、化学平衡のうち、閉じた系と周囲との間で物質の直接接触や物質の移動がないので、系と周囲の関係で相平衡、化学平衡については考える必要がなく、熱平衡と力学平衡について考える。 ^3.13。

まず系と周囲との間で力学平衡を成り立たせるための条件を考えよう。系と周囲が力学平衡にあれば系からピストンへの力と周囲からピストンへの力が等しい。ピストンの両端での力が等しい状況ではピストンは動かないため、系は変化しない。そこで準静的過程ではゼロの極限をとった微小な圧力差 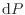$\mathrm{d}P$ [Pa]を考える。極微小な圧力差による変化ではピストンの移動量も極微小であり限りなくゼロに近い値となる。そのため、ピストンが動くには無限の時間が必要となる。このように、準静的過程では力学平衡を保ったまま（微少圧力差により）無限の時間をかけピストンを移動させる。

次に系と周囲の間で熱平衡を保ったままでの熱の移動を考える。系と周囲が熱平衡にあるとき、系と周囲の温度は等しい。系と周囲にゼロの極限をとった極微小な温度差 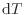$\mathrm{d}T$ [℃またはK]を考え、熱が伝わっている時間を無限大と考えれば、熱平衡を保ったまま（極微小な温度差により）無限の時間をかけて熱を伝えることができる。

系の内部で熱力学的平衡を維持するための条件を考えよう。系の内部で、熱平衡が成り立つためには温度分布がなく、力学平衡のためには圧力分布がなく渦などの流れはない状態とならなくてはならない。極限をとった微小な温度変化や圧力変化であれば、常に温度分布・圧力分布がなく熱平衡・力学平衡が維持されていると考えられる。

上記のように、微小な圧力差と微小な温度差により熱力学的平衡を維持したまま、無限の時間をかけて系を変化させる可逆過程が準静的過程である。準静的過程では無限の時間が必要であり、現実では不可能な仮想的な過程である。準静的過程におけるゼロの極限をとった微小な差の詳細については、付録 $^{\text{p.\pageref{sec-QuasiStaic}}}$ に記す。また、準静的過程が可逆となり、準静的過程でないと不可逆過程となる理由については、付録 $^{\text{p.\pageref{sec-AppendixIrreversible}}}$ に記す。

• 学問 -top-

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。