


Next: 2.1.3 非定常項
Up: 2.1 保存量
Previous: 2.1.1 支配方程式
2.1.2 コントロールボリューム
微小なコントロールボリューム(図2.1)を考える。コントロールボリュームの各境界面での値を表す変数(速度や温度)には下付文字をつけて表す。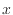 方向に垂直な左側の面は下付
方向に垂直な左側の面は下付 で、右側の面は下付
で、右側の面は下付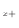 で、
で、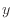 方向に垂直な下側の面は下付
方向に垂直な下側の面は下付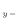 で、上側の面は下付
で、上側の面は下付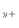 で、
で、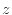 方向に垂直な奥側の面は下付
方向に垂直な奥側の面は下付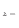 で、手前側の面は下付
で、手前側の面は下付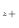 で表される。下付きのない変数はコントロールボリュームでの代表値の値とする。
で表される。下付きのない変数はコントロールボリュームでの代表値の値とする。
コントロールボリュームのそれぞれの面について、コントロールボリュームの各面に面積ベクトルをとると以下のように書ける。面積ベクトルとは、対象とする面の単位法線ベクトルに面積をかけたベクトルである。
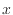 軸に垂直
軸に垂直 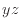 面左
面左-
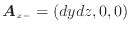 |
(2.1) |
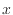 軸に垂直
軸に垂直 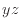 面右
面右-
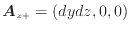 |
(2.2) |
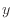 軸に垂直
軸に垂直 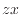 面下
面下-
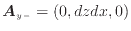 |
(2.3) |
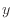 軸に垂直
軸に垂直 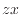 面上
面上-
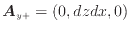 |
(2.4) |
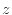 軸に垂直
軸に垂直 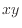 面後
面後-
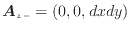 |
(2.5) |
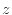 軸に垂直
軸に垂直 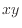 面前
面前-
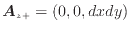 |
(2.6) |



Next: 2.1.3 非定常項
Up: 2.1 保存量
Previous: 2.1.1 支配方程式
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![\includegraphics[width=50mm]{figures/ControlVolume.eps}](img27.png)