• 学問 -top-

2.1.3 非定常項

式(2.1)において、"コントロールボリューム内に持っている物理量の時間変化"は

$$コントロールボリューム内に持っている物理量の時間変化 = \frac{\partial 持っている物理量}{\partial t}$$

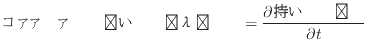
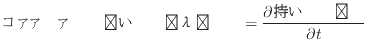
と表す。この項を非定常項と呼び、増加するとコントロールボリューム内の保存量が増加し、運動量であれば、速度が速くなる。

例として図2.2のような排出口のある水槽をコントロールボリュームとして、考えてみる。

図 2.2: Control Volume Water

支配方程式をたてる対象の物理量を水の体積[m$^3$ ]とする。"コントロールボリューム内に持っている物理量の時間変化"は水槽に溜まっている水の量$V$ [m$^3$ ]の時間変化 $\dfrac{\partial V}{\partial t}$ [m$^3$ /s]で表される(ここで$t$ [s]は時間)。式(2.1)における"時間あたりに境界面でコントロールボリュームに出入りする物理量"は水槽に入る水と出る水の差なので $F_{in}-F_{out}$ [m$^3$ /s]で表される。水槽の中での水の生成や消滅は考えないので、この水槽をコントロールボリュームとした水の体積に対する支配方程式は次の式で表される。

$$\frac{\partial V}{\partial t} = F_{in}-F_{out}$$

水槽が密閉されており中の水の様子が観察できない場合でも、上式に水の流入量と流出量を代入することにより、水の体積の変化を知ることができる。

他の例として、物理量が運動量で左辺が正の値（物理量が増加する）であれば、コントロールボリュームでの速度が増加する。物理量がエネルギーであれば、コントロールボリュームでの温度が上昇する。流入量と流出量が等しければ、右辺の合計はゼロとなり、水の体積の時間変化がなくなる。この時、時間に対して変化せず定常状態となる。

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。