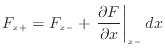


Next: 2.2 質量保存
Up: 2.1 保存量
Previous: 2.1.6 相対する面での差の計算
2.1.7 微小項の取り扱い
微小体積のコントロールボリュームを考えている(2.1.3節)ため、体積は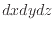 で表される。コントロールボリュームの体積あたりの微小量(
で表される。コントロールボリュームの体積あたりの微小量(
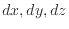 )は計算対象となる項に比べ高位の無限小となるため、式中の次の項(
)は計算対象となる項に比べ高位の無限小となるため、式中の次の項(
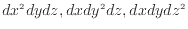 )は無視する。
)は無視する。
また、項が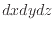 で括られている、または式全体を
で括られている、または式全体を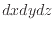 で割った場合には、各境界面の間での変数の値の差は計算対象となる項と比べ高位の無限小であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.11)
で割った場合には、各境界面の間での変数の値の差は計算対象となる項と比べ高位の無限小であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.11)
 p.
p.![[*]](crossref.png) で表されるx軸に垂直な面の左側と右側での差を考える。式(2.11)よりx軸に垂直な面の左側と右側での変数
で表されるx軸に垂直な面の左側と右側での差を考える。式(2.11)よりx軸に垂直な面の左側と右側での変数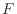 の関係は以下のようになる。
の関係は以下のようになる。
これがコントロールボリュームの体積あたりの値(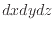 で割った式)であるとすれば、右辺第二項は計算対象の項と比べ高位の無限小であるので、無視し、次式のようにx軸左側と右側の値が等しくなり、下付をつけないコントロールボリュームの代表値として表される。
で割った式)であるとすれば、右辺第二項は計算対象の項と比べ高位の無限小であるので、無視し、次式のようにx軸左側と右側の値が等しくなり、下付をつけないコントロールボリュームの代表値として表される。



Next: 2.2 質量保存
Up: 2.1 保存量
Previous: 2.1.6 相対する面での差の計算
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![[*]](crossref.png) で表されるx軸に垂直な面の左側と右側での差を考える。式(2.11)よりx軸に垂直な面の左側と右側での変数
で表されるx軸に垂直な面の左側と右側での差を考える。式(2.11)よりx軸に垂直な面の左側と右側での変数![]() で括られている、または式全体を
で括られている、または式全体を![]() で割った場合には、各境界面の間での変数の値の差は計算対象となる項と比べ高位の無限小であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.11)
で割った場合には、各境界面の間での変数の値の差は計算対象となる項と比べ高位の無限小であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.11)
![]() p.
p.![[*]](crossref.png) で表されるx軸に垂直な面の左側と右側での差を考える。式(2.11)よりx軸に垂直な面の左側と右側での変数
で表されるx軸に垂直な面の左側と右側での差を考える。式(2.11)よりx軸に垂直な面の左側と右側での変数![]() の関係は以下のようになる。
の関係は以下のようになる。