


Next: 2.1.7 微小項の取り扱い
Up: 2.1 保存量
Previous: 2.1.5 出入の項 面での作用
2.1.6 相対する面での差の計算
式(2.4)
 p.
p.![[*]](crossref.png) で表さられる支配方程式の出入量について考える。コントロールボリューム内の物理量が増えると正となるので出入は“入る量 - 出る量”で計算される。
図2.2の左側のyz面で、物理量の出入
で表さられる支配方程式の出入量について考える。コントロールボリューム内の物理量が増えると正となるので出入は“入る量 - 出る量”で計算される。
図2.2の左側のyz面で、物理量の出入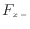 があるとする。このときの、右のyz面での出入を考える。yz面を通過する出入の量が
があるとする。このときの、右のyz面での出入を考える。yz面を通過する出入の量が の位置によって異なれば、
の位置によって異なれば、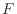 はxの関数として表される。コントロールボリューム左側から右側に
はxの関数として表される。コントロールボリューム左側から右側に 方向の位置が
方向の位置が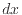 だけ変わるとき、それぞれでの出入の量、
だけ変わるとき、それぞれでの出入の量、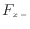 と
と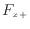 の値はどう違うだろうか。図2.4に示すように、左側の面での流量
の値はどう違うだろうか。図2.4に示すように、左側の面での流量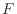 の
の 方向への変化量(傾き)は、
方向への変化量(傾き)は、 で微分した値、
で微分した値、
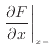 となる。図2.4のグラフのように傾きは
となる。図2.4のグラフのように傾きは
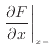 であるので、dx離れた右側の位置での縦軸の
であるので、dx離れた右側の位置での縦軸の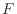 の微小変化量
の微小変化量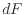 は、傾きに
は、傾きに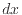 をかけた
をかけた
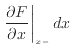 となる。よって、右側の面での出入の量、
となる。よって、右側の面での出入の量、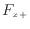 は次のように表される2.4。
は次のように表される2.4。
x方向のyz面における出入の量は、これらの左側の面での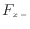 と右側の面での
と右側の面での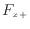 から求められる。出入量は左側と右側の面ではコントロールボリュームに対して出る方向と入る方向が逆になるので、差をとりx方向の値を求める。例えば左から右(xの正の方向)に物理量が移っている場合は、左の面では入る方向で増加するプラス、右の面では出て行き減少しマイナスとなる。式で表すと、
から求められる。出入量は左側と右側の面ではコントロールボリュームに対して出る方向と入る方向が逆になるので、差をとりx方向の値を求める。例えば左から右(xの正の方向)に物理量が移っている場合は、左の面では入る方向で増加するプラス、右の面では出て行き減少しマイナスとなる。式で表すと、
となる。式(2.4)
 の“境界面での対流による出入量”、“境界面での作用による出入量”、“体積に対する変化量”の項は上式(2.12)
の“境界面での対流による出入量”、“境界面での作用による出入量”、“体積に対する変化量”の項は上式(2.12)
 で表される。入ってくる物理量をベクトルで表すと、変化量は発散2.5で表される。
で表される。入ってくる物理量をベクトルで表すと、変化量は発散2.5で表される。



Next: 2.1.7 微小項の取り扱い
Up: 2.1 保存量
Previous: 2.1.5 出入の項 面での作用
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
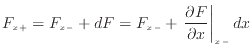
![[*]](crossref.png) で表さられる支配方程式の出入量について考える。コントロールボリューム内の物理量が増えると正となるので出入は“入る量 - 出る量”で計算される。
図2.2の左側のyz面で、物理量の出入
で表さられる支配方程式の出入量について考える。コントロールボリューム内の物理量が増えると正となるので出入は“入る量 - 出る量”で計算される。
図2.2の左側のyz面で、物理量の出入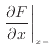 となる。図2.4のグラフのように傾きは
となる。図2.4のグラフのように傾きは
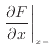 であるので、dx離れた右側の位置での縦軸の
であるので、dx離れた右側の位置での縦軸の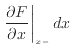 となる。よって、右側の面での出入の量、
となる。よって、右側の面での出入の量、![]() と右側の面での
と右側の面での![]() から求められる。出入量は左側と右側の面ではコントロールボリュームに対して出る方向と入る方向が逆になるので、差をとりx方向の値を求める。例えば左から右(xの正の方向)に物理量が移っている場合は、左の面では入る方向で増加するプラス、右の面では出て行き減少しマイナスとなる。式で表すと、
から求められる。出入量は左側と右側の面ではコントロールボリュームに対して出る方向と入る方向が逆になるので、差をとりx方向の値を求める。例えば左から右(xの正の方向)に物理量が移っている場合は、左の面では入る方向で増加するプラス、右の面では出て行き減少しマイナスとなる。式で表すと、