粘性係数(粘度)と動粘性係数(動粘度)の違い
粘性係数(粘度) Dynamic viscosityと動粘性係数(動粘度) Kinematic viscosityはともに物質と状態が決まれば値が決まる物性値であり、流体(気体と液体)の性質を表す。
1 粘性係数
粘性係数は流体に働く粘性力の強さを表している。流体の流れがあり、その中で速度に違いがあると、図1に示すように速度が速い流体は遅く(図中赤点線矢印)、速度の遅い流体は早くする方向(図中赤実線矢印)に粘性力が働く。 このときに流体間に働く力は単位面積あたりの応力 (単位:N/m
(単位:N/m ) 1として速度
) 1として速度 (単位:m/s) の勾配と粘性係数
(単位:m/s) の勾配と粘性係数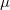 (単位:Pa s) より次式のように表される。
(単位:Pa s) より次式のように表される。
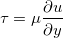 |
粘性係数は上式によって定義される流体の粘性力の伝わりやすさを表した値である。
![\includegraphics[width=50mm]{figures/Viscosity.eps}](images/img-0006.png)
注
- 文中で理解を深めるため、それぞれの変数のSI(国際単位系)における単位を (単位:) により表す。
2 動粘性係数
動粘性係数は速度の拡散しやすさと捉えることができる。しかし、速度の拡散とはどんな性質を表しているのか少し分かりにくい。そこで静止した水の中に手を入れて動かした場合を例として考える。静止した水に力を加える(手を入れて動かす)とまず力を加えた箇所の水が動き出す。動き出した水と周囲の静止した水の間に働く粘性力により、周囲の水も動き出す。粘性により力が伝わり、力を受けた周囲の水は動きだし、速度が進行方向と垂直に拡散するように見える。動粘性係数はこの速度の拡散のしやすさを表した値である。速度の伝わりやすさ(動粘性係数)は力の伝わりやすさ(粘性係数)と密度によって決まる。粘性係数が大きいと大きな力が伝わるが、物質の質量(密度)が大きければ大きな力が加わっても速度は大きく変化しない。質量(密度)が小さければ大きな力でなくても速度も大きく変化し、遠くまで速度の変化が拡散する。このことから動粘性係数 (単位:m
(単位:m /s) は次式のように粘性係数
/s) は次式のように粘性係数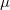 (単位:Pa s) を密度
(単位:Pa s) を密度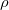 (単位:kg/m
(単位:kg/m ) で割ることで定義されている。
) で割ることで定義されている。
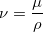 |
(1) |
3 違い
粘性係数の表す力の拡散と動粘性係数の表す速度の拡散はどう違うのだろうか。粘性力と速度の拡散を図2に示すように四種類の流体(液体か気体)を仮定して考える。流体1は粘性係数が大きく密度が小さい(式(1)より動粘性係数は大きくなる)、流体2は粘性係数が大きく密度が大きい(式(1)より動粘性係数は小さくなる)、流体3は粘性係数が小さく密度が小さい(動粘性係数は流体2と同じ程度に小さいとする)、流体4は粘性係数が小さく密度が大きい(式(1)より動粘性係数は極めて小さくなる)。図2に示すように、この4種類の流体の中に壁があり、その壁が突然動いた時の流体の力の作用と速度の変化を考える。壁が動き出すと、粘性係数の大きな流体1、流体2では流体に大きな粘性力(図中赤矢印)が働き、粘性係数の小さな流体3と流体4では比較的小さな力が働く。流体に力が働くと動きだし、速度が生じる。密度の小さい流体1では流体は壁に近い速度で動き出す。流体2では密度が大きく重いため同じ力が働いても流体1よりも速度は遅くなる。流体3では力は小さいが密度も小く軽いため流体2と同じ程度の速度となる。流体4では力が小さく密度が大きいため速度は極めて遅くなる。力は図中下に向かって伝わり徐々に下方の流体に速度が生じていく。動粘性係数が大きな流体1では下の流体でも壁の速度に近い速度で動く。動粘性係数が小さい流体2と流体3では速度は壁に比べ遅くなる。流体2と流体3では粘性係数が異なるため働く粘性力は異なるが、動粘性係数が近いため流体の速度は近い速度分布となる。流体4では動粘性係数が極めて小さいので下方の流体の速度は壁に比べ極めて遅くなる。このように、粘性係数は力の伝わりやすさを表し、動粘性係数は速度の伝わりやすさを表している。
![\includegraphics[width=120mm]{figures/ViscosityDensity.eps}](images/img-0011.png)
4 具体例
空気と水の粘性係数、密度、動粘性係数の具体的な値(常圧、26.85 C(300K))を表1に示す(引用元:熱物性ハンドブック、日本熱物性学会、養賢堂、2008年)。表1のように水は空気に比べ粘性係数は高いが、動粘性係数は空気が高い。すなわち粘性力は水の方が伝えやすいが、空気のほうが簡単に遠くの流体まで動かすことができる。
C(300K))を表1に示す(引用元:熱物性ハンドブック、日本熱物性学会、養賢堂、2008年)。表1のように水は空気に比べ粘性係数は高いが、動粘性係数は空気が高い。すなわち粘性力は水の方が伝えやすいが、空気のほうが簡単に遠くの流体まで動かすことができる。
物質 |
粘性係数 / ( |
密度 / (kg/m |
動粘性係数 / (mm |
空気 |
18.57 |
1.176 |
15.79 |
水 |
853.8 |
996.56 |
0.857 |
5 熱伝導率と熱拡散率
熱伝導率と熱拡散率(温度伝導率)も同じ関係で、熱の拡散と温度の拡散をそれぞれ表してる。伝わった熱によってどれくらい温度が変化するかは、体積あたり単位温度上げるのに必要なエネルギーで熱を割ればよい。体積あたりの単位温度上げるのに必要なエネルギーは比熱に密度をかけると求められる。このことから熱伝導率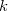 (単位:W/m K) を比熱
(単位:W/m K) を比熱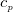 (単位:J/K kg) と密度
(単位:J/K kg) と密度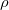 (単位:kg/m
(単位:kg/m ) で割ると熱拡散率
) で割ると熱拡散率 (単位:m
(単位:m /s) になる。
/s) になる。
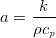 |
運動量(エネルギー)が力(熱)として伝わる(拡散する)。運動量(エネルギー)の拡散は速度(温度)の勾配があると力(熱)として伝わる。その力(熱)の伝わる大きさが物質により違い、粘性係数(熱伝導率)として表される。拡散は速度(温度)勾配によって起こるため、速度場(温度場)へ拡散が与える影響は速度(温度)の変化を表す動粘性係数(熱拡散率)として表される。直接測定することのできない力や熱が伝わった(拡散した)結果、測定できる速度や温度が変化する。この測定できる速度と温度の拡散は同じ単位 m /sで表される。
/sで表される。

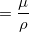
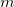 (単位:kg) の流体の運動量の時間変化はニュートンの第二法則より慣性力
(単位:kg) の流体の運動量の時間変化はニュートンの第二法則より慣性力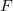 (単位:N) と呼ばれ、速度
(単位:N) と呼ばれ、速度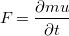
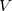 (単位:m
(単位:m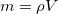 と表すことが出来る。ここで密度
と表すことが出来る。ここで密度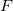
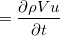

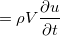
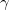 (単位:m/s) によって生じる。
(単位:m/s) によって生じる。 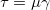
 方向、
方向、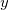 方向の二次元の流れとし、
方向の二次元の流れとし、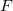 (単位:N) のみを考える。
(単位:N) のみを考える。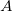 (単位:m
(単位:m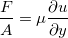
![\includegraphics[width=50mm]{figures/ControlVolume.eps}](images/img-0035.png)
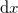 、
、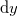 を持つ直方体を検査体積として考える。
を持つ直方体を検査体積として考える。 方向には計算上
方向には計算上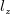 の長さを持つとする。 この検査体積に働く力は
の長さを持つとする。 この検査体積に働く力は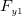 、
、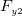 をそれぞれ求める。粘性力の作用する面の面積
をそれぞれ求める。粘性力の作用する面の面積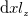 で表されるので、式(
で表されるので、式(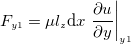
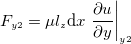
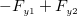
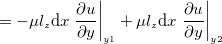
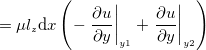
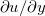 の関係を考える。
の関係を考える。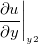
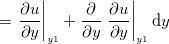
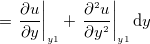
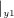 を外す。
を外す。 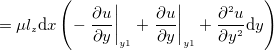
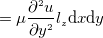
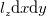 で表すことが出来る。
で表すことが出来る。 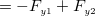
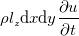
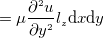
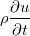
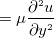

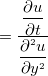

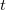 と
と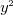 が残り、
が残り、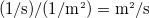 となる。
となる。 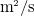 である。これはどの値も拡散のしやすさを拡散対象量の時間変化率(1/s)と勾配の勾配(1/m
である。これはどの値も拡散のしやすさを拡散対象量の時間変化率(1/s)と勾配の勾配(1/m