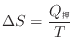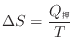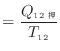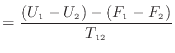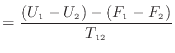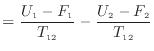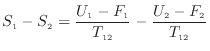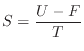


Next: 2.5 エンタルピー
Up: 2.4 エントロピー
Previous: 2.4.1 定義
可逆サイクルで伝わる熱によりエントロピーの変化は以下の式(2.6)で表される。
等温準静過程での熱は式(2.3)のように内部エネルギー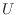 [J]とヘルムホルツの自由エネルギー
[J]とヘルムホルツの自由エネルギー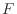 [J]で表され、式(2.6)は状態1から状態2へ変化する過程とすれば次のように変形できる。
[J]で表され、式(2.6)は状態1から状態2へ変化する過程とすれば次のように変形できる。
変化量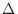 を差で表すと次式となる。
を差で表すと次式となる。
上式中で各状態ごとの状態量の関係を示すと、エントロピーを可逆の条件をつけることなく次式のように表せる。



Next: 2.5 エンタルピー
Up: 2.4 エントロピー
Previous: 2.4.1 定義
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。