条件1で示したように断熱された系が可逆変化した場合、エントロピー![]() は変化しないように定義したい。可逆断熱変化でのエントロピーの変化を
は変化しないように定義したい。可逆断熱変化でのエントロピーの変化を
![]() とすると次式で表される。
とすると次式で表される。
条件2の不可逆の変化で増加する性質を考える。熱が関わると現象は不可逆となる(1.3.2節 p.![[*]](crossref.png) )。
)。
熱力学第二法則クラウジウスの原理(1.3節 p.![[*]](crossref.png) )に定義されるように低温から高温へ他に影響を及ぼさず熱を伝えることはできない。温度差がある物体間で熱が伝わる場合は必ず不可逆となる(温度の高い物体から低い物体に熱は伝わるが、温度の低い物体から高い物体へは熱は伝わらない)。熱が発生する場合も不可逆である。例えば、系の内部では運動エネルギーが粘性消散2.1により熱となる。多くの場合で力学的エネルギーが内部エネルギーへ変化し、発生した熱が多い場合は不可逆な変化が大きい。そのため、熱量
)に定義されるように低温から高温へ他に影響を及ぼさず熱を伝えることはできない。温度差がある物体間で熱が伝わる場合は必ず不可逆となる(温度の高い物体から低い物体に熱は伝わるが、温度の低い物体から高い物体へは熱は伝わらない)。熱が発生する場合も不可逆である。例えば、系の内部では運動エネルギーが粘性消散2.1により熱となる。多くの場合で力学的エネルギーが内部エネルギーへ変化し、発生した熱が多い場合は不可逆な変化が大きい。そのため、熱量![]() [J]とエントロピーの変化量
[J]とエントロピーの変化量![]() が比例するように条件2は次のように表せる。
が比例するように条件2は次のように表せる。
条件3の全体は断熱された内部で熱のやり取りのある複数の系の場合を考える。高温物体と低温物体の間でカルノーサイクルを用いると、高温熱源から低温熱源へと熱が伝わる際に仕事を取り出し、逆の過程では仕事を与えて低温熱源から高温熱源へ熱を伝えることができる。カルノーサイクルではこのように仕事が作用することで可逆の過程で熱を伝えることができる。 高温熱源の系と低温熱源の系、カルノーサイクルが図2.1のように全体として断熱されているとき、カルノーサイクルの過程は可逆であるので、条件3が成り立つように、サイクルが動作しても全体としてエントロピーが増加しないようにエントロピーを定義したい。サイクルでは初めと終わりの状態が変わらないため状態は変化せず状態量も変わらない。そのためカルノーサイクルの系ではエントロピーは変化しない。 熱機関としての動作を考えると、高温熱源は熱を奪われるためエントロピーの減少を考え、低温熱源は熱を受け取るためエントロピーの増加を考える。この高温熱源の系でのエントロピーの減少と低温熱源の系でのエントロピーの増加が等しくなり、可逆過程であるので全体としてエントロピーが変化しないように定義する。
条件1条件2を満たすために、式(2.4)と式(2.5)の両方を満たし、条件3を満たすため可逆サイクルであるカルノーサイクルを含む系でエントロピーが変化しないように、エントロピーの定義をしたい。
カルノーサイクルでの熱源とやりとりをする熱と温度の関係は、式(1.27) p. ![[*]](crossref.png) より以下の式で表される。
より以下の式で表される。
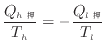 |
(1.27) |
図2.1に示す系で、高温熱源と低温熱源が有限の大きさであれば、カルノーサイクルから熱をやりとりすることで温度が変わるため、等温変化とならない。しかし、等温変化と見なせるように、熱源の温度の変化が十分に小さくなる微小な熱量![]() が高温
が高温![]() の系からカルノーサイクルへ伝わり、微小な熱量
の系からカルノーサイクルへ伝わり、微小な熱量![]() がカルノーサイクルから低温
がカルノーサイクルから低温![]() の系へ伝わったときを考える。高温の系で微小な熱量
の系へ伝わったときを考える。高温の系で微小な熱量![]() による微小なエントロピーの変化
による微小なエントロピーの変化![]() は次式で表される。
は次式で表される。
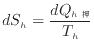
低温の系で微小な熱量
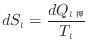
この状態で、カルノーサイクルでの温度と熱量の式(1.27)から次式のように高温の系でのエントロピーの減少量と低温の系でのエントロピーの増加量が等しくなる。
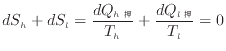
十分に小さな変化であれば、温度の変化も小さく等温過程と見なせる。十分に小さい可逆変化での
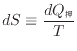 |
(2.6) |
1.7.2節 p. ![[*]](crossref.png) で示したように、準静等温過程であれば、
で示したように、準静等温過程であれば、![]() は内部エネルギーの変化量と前後の状態によってのみ決まるため、エントロピー
は内部エネルギーの変化量と前後の状態によってのみ決まるため、エントロピー![]() も前後の状態で変化量が決まり、状態量であると言える。
も前後の状態で変化量が決まり、状態量であると言える。