![\includegraphics[width=60mm]{figures/0thLaw.eps}](img294.png)
|
温度の基準として1990年国際温度目盛(ITS-90)[3]により、ネオンの三重点24.5561 Kや水の三重点273.16 Kなどが絶対温度の基準温度として決められている。この基準温度の間の温度を決めるための方法も必要である。長さや質量と違い、温度では基準の間の値を決めることが難しい。例えば、基準温度であるネオンの三重点24.5561 Kと水の三重点273.16 Kの物体が手元にある場合に、自分の体の温度が何度であるか知るためにはどうしたらいいだろうか。図2.3のように質量であれば、自分の質量を測る場合、基準となる1 kgの物体が複数個あれば、秤を使うことにより重量を比較し、ある程度の精度で質量を知ることができる。また、自分の長さを測る場合でも、基準となる0.1 mの物体が複数個あれば、2つで0.2 m、3つで0.3 mと基準となる物体に応じた精度で長さを知ることができる。しかし、温度の場合は24.5561 Kの基準が何個あっても、他の温度を測ることはできない(2つで49.1122 Kのように)。24.5561 Kの物体は何個あっても24.5561 Kのままである。では、現在流通されている温度計はどのように温度を測っているのだろうか。よく見かける棒温度計では内部の液体(水銀や赤色の色素の入ったエタノール)の体積が温度変化と共に変化することを利用し、体積に応じた温度を示している。しかし、この液体の体積と温度の関係は単純に温度が二倍になれば体積が二倍という変化ではなく、温度ごとに体積変化の傾向が違う。そのため、温度による体積変化を利用した棒温度計を作るには、体積と温度の関係を知る必要がある。温度との関係を知るためには、基準となる温度がなくてはならない。そのため、温度計を作るためには基準の間の温度を決める方法が必要である。
その基準の間の温度は絶対温度![]() [K]として1.5.3節の式(1.32) p.
[K]として1.5.3節の式(1.32) p. ![[*]](crossref.png) で示す可逆サイクルであるカルノーサイクルの熱源とのやりとりする熱量の比で国際的に定義されている[3]。
で示す可逆サイクルであるカルノーサイクルの熱源とのやりとりする熱量の比で国際的に定義されている[3]。
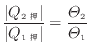 |
(1.32) |
![[*]](crossref.png) に示したように次式で国際的にSI単位系において組立単位として定義されている[4]。
に示したように次式で国際的にSI単位系において組立単位として定義されている[4]。