next up previous contents
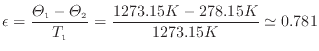
Next: 2. 閉じた系 Up: 1.4 可逆熱機関（可逆ヒートポンプ） Previous: 1.4.8 問題

1.4.9 解答

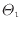可逆熱機関の効率は式(1.32)（p. [*]）で表される。二つの熱源の差が大きいほど効率は良くなるため、5℃と1000℃の組み合わせが最も効率が高くなる。式(1.32)中 $ \varTheta_1$ [K]が高温熱源温度、 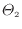$ \varTheta_2$ [K]が低温熱源の温度であるので、それぞれ求める。

$\displaystyle T_1$ $\displaystyle = 1000 + 273.15 = 1273.15 K$    
$\displaystyle T_2$ $\displaystyle = 5 + 273.15 = 278.15 K$    

$\displaystyle \epsilon = \frac{\varTheta_1 - \varTheta_2}{T_1} = \frac{1273.15 K - 278.15 K}{1273.15 K} \simeq 0.781 $

効率は0.781である。
next up previous contents
Next: 2. 閉じた系 Up: 1.4 可逆熱機関（可逆ヒートポンプ） Previous: 1.4.8 問題

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。