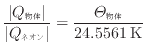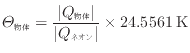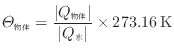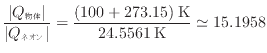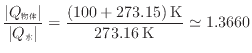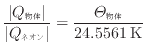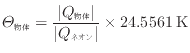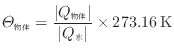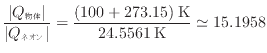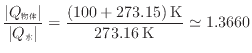


Next: 3. 閉じた系
Up: 2.4 温度
Previous: 2.4.2 問題
- 基準温度であるネオンか水のどちらかと、温度のわからない物体間で可逆の熱機関を動作させる。ネオンと温度のわからない物体間で可逆サイクルを動作させると、可逆サイクルからネオンへ伝わる熱量
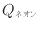 [J]、物体に伝わる熱量
[J]、物体に伝わる熱量
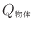 [J]、物体の絶対温度
[J]、物体の絶対温度
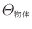 [K]の関係は式(1.32)
[K]の関係は式(1.32)
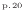 より次のように表される。
より次のように表される。
上式を変形し、物体の温度は次式で求められる。
水を基準とした場合には次式となる。
伝わった熱量を測定し、その比を求めて上式に入れることで温度を求めることができる。
- 前問と同様、式(1.32)
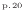 よりネオンを基準とすると次式が成り立つ。
よりネオンを基準とすると次式が成り立つ。
水を基準とすれば次のようになる。



Next: 3. 閉じた系
Up: 2.4 温度
Previous: 2.4.2 問題
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。