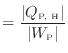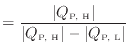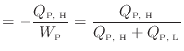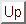


Next: 1.4.3 可逆熱機関と可逆ヒートポンプ
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.1 熱機関とヒートポンプ
ここでは高温熱源と低温熱源の二つの熱源の間で動作する熱機関とヒートポンプを考える(1.1節
 も参照)。図1.4に二つの熱源で動作する熱機関とヒートポンプの概要を示す。熱機関では高温熱源から熱
も参照)。図1.4に二つの熱源で動作する熱機関とヒートポンプの概要を示す。熱機関では高温熱源から熱
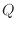 E, H
[J]を受け取り、一部を仕事
E, H
[J]を受け取り、一部を仕事
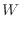 E
[J]として取り出し、残りの熱
E
[J]として取り出し、残りの熱
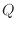 E, L
[J]を低温熱源へ伝えている。ヒートポンプでは一定温度の低温熱源から熱
E, L
[J]を低温熱源へ伝えている。ヒートポンプでは一定温度の低温熱源から熱
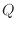 P, L
[J]を受け取り、仕事
P, L
[J]を受け取り、仕事
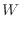 P
[J]をされることで、熱
P
[J]をされることで、熱
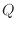 P, L
[J]を一定温度の高温熱源へ伝えている。図1.4では二つの○がそれぞれ熱機関とヒートポンプを表し、高温熱源と低温熱源にそれぞれ接しており矢印で熱と仕事を表している。
P, L
[J]を一定温度の高温熱源へ伝えている。図1.4では二つの○がそれぞれ熱機関とヒートポンプを表し、高温熱源と低温熱源にそれぞれ接しており矢印で熱と仕事を表している。
この二つの熱源間で動作する熱機関とヒートポンプの効率を定義しよう。熱と仕事は入るものを正、出るものを負としている。熱機関とヒートポンプは内部エネルギーの変化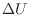 [J]がゼロ(温度は時間的に変化しない)と考える。第一法則(式(1.7)
[J]がゼロ(温度は時間的に変化しない)と考える。第一法則(式(1.7)
 )より熱機関では高温熱源から受け取る熱
)より熱機関では高温熱源から受け取る熱
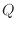 E, H
[J](正の値)と低温熱源に移す熱
E, H
[J](正の値)と低温熱源に移す熱
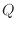 E, L
[J](負の値)、得られる仕事
E, L
[J](負の値)、得られる仕事
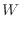 E
[J](負の値)の関係は
E
[J](負の値)の関係は
絶対値で表すと以下のようになる。
熱機関では仕事を取り出すことが目的であるので、少ない高温熱源からの熱で多くの仕事に変換出来ると効率がよいといえる。そこで、熱機関の効率
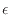 E
[-]は
E
[-]は
で定義される。また、式(1.8)より
となる。絶対値を外すと
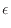
E
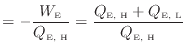
と定義される。
第一法則(式(1.7)
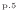 )よりヒートポンプでは低温熱源から受け取る熱
)よりヒートポンプでは低温熱源から受け取る熱
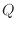 P, L
[J](正の値)と高温熱源へ移す熱
P, L
[J](正の値)と高温熱源へ移す熱
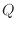 P, H
[J](負の値)、必要な仕事
P, H
[J](負の値)、必要な仕事
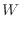 P
[J](正の値)1.11の関係は
P
[J](正の値)1.11の関係は
絶対値により次のように表される。
ヒートポンプでは低温熱源から高温熱源へ熱を伝えるのが目的であるので、少ない仕事で多くの熱を移せると効率がよいといえる。そこで、ヒートポンプの効率
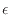 P
[-]は
P
[-]は
で定義される。また、式(1.11)より
となる。絶対値を外すと
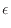
P
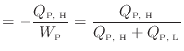
と定義される1.12。



Next: 1.4.3 可逆熱機関と可逆ヒートポンプ
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.1 熱機関とヒートポンプ
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![\includegraphics[width=75mm]{figures/HeatEnginePumpSource.eps}](img133.png)
![]() [J]がゼロ(温度は時間的に変化しない)と考える。第一法則(式(1.7)
[J]がゼロ(温度は時間的に変化しない)と考える。第一法則(式(1.7)
![]() )より熱機関では高温熱源から受け取る熱
)より熱機関では高温熱源から受け取る熱
![]() E, H
[J](正の値)と低温熱源に移す熱
E, H
[J](正の値)と低温熱源に移す熱
![]() E, L
[J](負の値)、得られる仕事
E, L
[J](負の値)、得られる仕事
![]() E
[J](負の値)の関係は
E
[J](負の値)の関係は
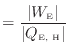
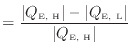
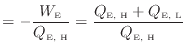
![]() )よりヒートポンプでは低温熱源から受け取る熱
)よりヒートポンプでは低温熱源から受け取る熱
![]() P, L
[J](正の値)と高温熱源へ移す熱
P, L
[J](正の値)と高温熱源へ移す熱
![]() P, H
[J](負の値)、必要な仕事
P, H
[J](負の値)、必要な仕事
![]() P
[J](正の値)1.11の関係は
P
[J](正の値)1.11の関係は