...この章では熱と仕事とサイクルについて述べる。仕事は容易に熱に変換できるが、熱は仕事に変換しづらい。また、熱が関わると現象は不可逆となる。この熱から仕事へ変換する機械が熱機関であり、熱力学の成立の背景には熱機関の効率を良くするという目的があった。熱機関は、蒸気を利用した蒸気機関車や、現在では自動車のエンジンや火力発電所、原子力発電所で利用され、高温熱源(燃料の燃焼など)と低温熱源(多くの場合、大気や海水)
1.1
自動車のエンジンを例に取ると低温熱源は大気である。低温の大気と高温の燃焼温度との間に温度差があるため、圧力差が生じエンジンが動作する。燃焼温度と大気温度が同じ温度であれば圧力差は生じず、エンジンのピストンは動かない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]は次のようになる
1.2
微小な仕事は連続関数の微小な変化ではなく、不完全微分であるので、"d"ではなく"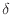 "で微小量を表す。
"で微小量を表す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
仕事は、ある物体から別の物体へ力が作用した際に伝わるエネルギーである。熱機関において、外部へされた仕事は運動エネルギーへと変換されることが多い1.3
仕事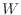 [J]をされた質量
[J]をされた質量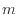 [kg]の速度
[kg]の速度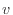 [m/s]で運動している物体の運動エネルギーの変化を示す。力
[m/s]で運動している物体の運動エネルギーの変化を示す。力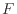 [N]は運動量の微小時間変化
[N]は運動量の微小時間変化
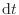 [s]により次式で定義される。通常、質量
[s]により次式で定義される。通常、質量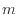 は一定と考えられるので、
は一定と考えられるので、
微小幅
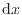 [m]の間、力を加えたときの仕事
[m]の間、力を加えたときの仕事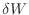 [J]は上式より次式で表される。
[J]は上式より次式で表される。
ここで、
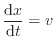 なので、
なので、
仕事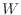 [J]が状態0
から状態
[J]が状態0
から状態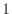 まで作用するときに、その区間で積分すると、
まで作用するときに、その区間で積分すると、
この
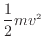 [J]が運動エネルギーである。仕事をされることにより物体の運動エネルギーは増加する。
[J]が運動エネルギーである。仕事をされることにより物体の運動エネルギーは増加する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
となる1.4
式(1.1)のように熱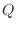 [J]は系に入り内部エネルギーが増加する条件で正、系から出て内部エネルギーが減少する条件で負とする。
[J]は系に入り内部エネルギーが増加する条件で正、系から出て内部エネルギーが減少する条件で負とする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...K)]
1.5
定積比熱とは体積の変化しない状態で単位質量(1 kg)の物体を単位温度(1 ℃)上昇させるのに必要なエネルギー量である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...K)]を一定とみなすことが出来れば
1.6
定積比熱などの物性値は温度と圧力で値が変化するが、ここではその変化量が小さいために一定とみなせるとする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]は次式より求まる
1.7
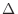 で表される変化量は変化後から変化前を引くことで求められる。前後の順番が分からなくなった時は、量が増加した場合は正の値となり、減少した場合は負の値となる順番にすると正しい式となる。
で表される変化量は変化後から変化前を引くことで求められる。前後の順番が分からなくなった時は、量が増加した場合は正の値となり、減少した場合は負の値となる順番にすると正しい式となる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...に示すように等しく、また高温の物体の内部エネルギーの変化したエネルギーが熱となって伝わり低温の物体の内部エネルギーを上昇させるため、高温の物体と低温の物体の内部エネルギーの変化量の絶対値は等しく次の関係が成り立つ
1.8
式(1.6)での熱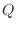 [J]は高温物体と低温物体どちらの出入りを考えるかで符号が変化するため絶対値で表す。また、低温物体での内部エネルギーの変化は増加するため正、高温物体は減少するため負となるので、高温物体の変化量にマイナスをつけることで式(1.6)が成り立つ。
[J]は高温物体と低温物体どちらの出入りを考えるかで符号が変化するため絶対値で表す。また、低温物体での内部エネルギーの変化は増加するため正、高温物体は減少するため負となるので、高温物体の変化量にマイナスをつけることで式(1.6)が成り立つ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fig-2ndLawThomson)。ある温度の物体とそれよりも低いもしくは高い温度の物体の間で熱機関を動作させると、高温から低温へ伝わる熱の一部を仕事として取り出すことができる。しかし温度差のない一つの物体から熱を取り出し仕事に変換するだけで、他には何も結果を残さないような過程は実現不可能であることを表しているのがトムソンの原理である。このトムソンの原理に反する装置があり、それを例えば船に載せたと考える。この際、このトムソンの原理に反する装置は、一様な温度を持つ物体である周囲の海水から熱を取り出し、仕事に変換し船を動かすことができる。船が停止すれば、船にされた仕事は全て熱として海へ戻るので、エネルギーは保存され熱力学第一法則には反しない。このようにトムソンの原理に反する装置があれば、燃料を使うことなく周囲の海水や大気から熱を取り出すことで乗り物を動かすことができる。しかし、トムソンの原理に反する装置が存在する可能性は今までに示されていない
1.9
一定温度の環境下でピストンを引いた際には一つの熱源から熱を取り出し、仕事に変換することができる。この際、一定温度の環境は一つの熱源と考えることができる。このように、一つの熱源から熱を取り出して仕事に変換することは出来るが、過程の前後で状態が変わってしまう(ピストンの位置が違う)ため、“ほかには何の結果も残さない”ことにはならない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
また、系の内部で流れがある場合には運動エネルギーが粘性消散1.10
流れで渦が発生し徐々に小さな渦となり、粘性により渦の運動エネルギーが熱に変換される
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J](正の値)1.11
必要な仕事の大きさは3.1.6節
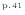 の
の
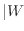 14
14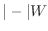 32
32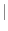 [J]にあたる
[J]にあたる
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
と定義される1.12
高温熱源側を利用する場合はヒートポンプと呼ばれる。また、低温熱源側を利用する場合は冷凍機と呼ばれ、効率の分子は低温熱源とやりとりする熱量
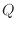 L
[J]となる。またヒートポンプや冷凍機の効率はCOP(Coefficient of Performance)とも呼ばれる。
L
[J]となる。またヒートポンプや冷凍機の効率はCOP(Coefficient of Performance)とも呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
効率の高い可逆熱機関(可逆ヒートポンプ)Aを熱機関として、可逆熱機関(可逆ヒートポンプ)Bをヒートポンプとして、仕事の大きさが同じになるように動作させ1.13
それぞれの熱機関(ヒートポンプ)の仕事の大きさが違う場合は、同じ熱機関(ヒートポンプ)を複数個まとめて動作させて、それぞれの数を調整し、総計で同じ仕事となるように調整する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...以上のように、熱機関としてもヒートポンプとしても同じ効率で動作できる可逆熱機関(可逆ヒートポンプ)では逆の働きをさせることが出来るため、可逆熱機関や可逆ヒートポンプの効率よりも不可逆熱機関や不可逆ヒートポンプの効率が高いと熱力学の第二法則クラウジウスの原理に反する。このことから、同じ二つの熱源間で動作する可逆熱機関(可逆ヒートポンプ)の効率は必ず不可逆熱機関や不可逆ヒートポンプの効率よりも高くなる
1.14
ここでの可逆熱機関(ヒートポンプ)と不可逆熱機関(ヒートポンプ)との比較は、(前節のような可逆と可逆でも)片方が可逆であり逆に動作させることが出来るため熱機関とヒートポンプの組み合わせにでき、全体の熱の移動に対してクラウジウスの原理を用いることができる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[℃またはK])の関数となる1.15
可逆熱機関(可逆ヒートポンプ)の効率が二つの熱源温度の組み合わせによらず一定であれば、この関数は温度によらない定数となる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]になるよう
1.16
伝わる熱の大きさを同じにするように、可逆熱機関Bと可逆熱機関Cを複数個一緒に動作させ、それぞれの可逆熱機関の数を調整する。複数の可逆熱機関を一つの可逆熱機関として考えれば、伝わる熱の大きさを等しくすることが出来る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
となる1.17
ここで関数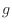 (関数
(関数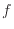 )が温度によらず一定であると成り立たないため、関数
)が温度によらず一定であると成り立たないため、関数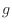 (関数
(関数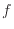 )は定数ではない。
)は定数ではない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...1991NRLM1.18
熱力学的温度(絶対温度)の詳細は2.4.1節
 に記す
に記す
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[kg]
2.1
化学の分野では質量の代わりにモル数[mol]を用いる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Properties)と呼ばれる2.2
系の状態の強さを表す示強性状態量は温度と圧力のみである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
状態量が独立ではない場合、例えば、圧力と温度は蒸発などの相変化をしているときにはどちらかが決まれば他方も決まり、独立な状態量ではないため相変化中の平衡状態を表すことができない2.3
相の数と独立な状態量の数の関係はギブスの相律で表される。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...1991NRLMにより、ネオンの三重点2.4
三重点とは三相(例えば気相・液相・固相)が共存する状態である。ギブスの相律により三相が共存する状態では温度と圧力が変化しない。二相状態では温度と圧力どちらかのみ変化できる(水の沸点は圧力が決まれば温度が決まり、沸騰する状態は点ではなく線で表される)。単相状態ではどんな温度、圧力の状態でもとれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...を読み取り上式へ代入することで温度を測定できる。2.5
物体と参照物質のどちらを高温側にするかは、物体の温度によって変える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
外部と物質の出入りがないが熱や仕事のやりとりはある系を“閉じた系”という3.1
外部と物質の出入りがなく熱や仕事のやりとりもない系を“孤立系”という。外部と物質の出入りも熱や仕事のやりとりもある系を“開いた系”という。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... を考える3.2
熱力学的な取り扱いをする際、系の状態は熱力学的平衡が成り立っている必要がある。しかし、ある平衡状態から次の平衡状態へ変化する間の過程では必ずしも常に平衡状態が維持されている必要はない。変化中の非平衡の系を扱うことはできないが、変化前の平衡状態と変化後の平衡状態の系の変化については取り扱うことが出来る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fig-ClosedSystemProcessのようにピストン形状の系を考える。ピストンの可動壁に壁を支える支持棒がついていると考え、系の圧力と釣り合うように支持棒に力を加える。仕事のやりとりのない過程では、固定して動かないようにする。通常系の外の空気などの流体によりピストンの外側には圧力が作用するが、ここでは考えやすくするため大気圧のような圧力はなく支持棒のみの力で支えられているとする
3.3
系外の流体の圧力が異なると支持棒の力が変わる。系が周囲にする仕事と、大気圧のような系外の流体に対する仕事と支持棒に対する仕事の和が等しくなるように、支持棒での仕事を変化させる。そのため、系外の流体の圧力の変化による系の周囲へする仕事への影響はない。指示棒と系外の流体にした仕事の和が系が周囲にした仕事である。
ただし現実の熱機関では、取り出せる仕事は支持棒への仕事であり、系が周囲へした仕事から系外の流体(大気など)にした仕事の量だけ減少する。
系の圧力と系外の流体の圧力、支持棒に加える力と仕事については付録B.1
 に詳細を示す。
に詳細を示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)ため、熱源はある一定の温度で一様な分布である必要がある。このため熱源の温度はすべて同じある一定の温度である3.4
現実的な熱源は有限の大きさであるため熱のやり取りをすれば温度が変化するが、ここでは理想的な無限の大きさの熱源を考え、熱のやり取りをしても温度の変化は十分に小さく無視できるとする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fig-Isometric)。この過程では系と周囲(熱源)の温度が異なり、高温側から低温側へと熱が伝わる。熱力学的平衡状態の系を熱源に接触させ、非平衡で熱が伝わり、(系と熱源を離し、十分に時間が経った後)系内部が熱力学的平衡となってから過程を終了する
3.5
過程の始めと終わりの状態は熱力学的平衡状態でなくてなはらない(3.1.1節
 )。
)。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fig-Isothermal)。周囲の熱源の温度は常に一定の温度である
3.6
周囲の熱源が有限の大きさであれば、熱を受け取れば温度が上がり熱を奪われれば温度が下がる。しかし、ここでは無限の大きさの周囲の熱源を考え熱のやり取りによる温度の変化は十分に小さいと考える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... [J]の仕事を周囲にしている3.7
絶対値を外すと
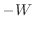 41
41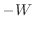 23
23
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
ガソリンエンジンでは作動流体が熱源となる。低温側では低温熱源となる大気を直接サイクルに取り込み、高温側では作動流体を直接燃焼させることで高温熱源とする。作動流体が熱源となるので、熱源と作動流体で熱交換をする必要がない3.8
他の熱交換をするサイクルの場合は、熱源と作動流体で熱交換をする際に必ず温度差が必要となるため、高温側で作動流体の温度は高温熱源より低く、低温側では低温熱源よりも高くなり、作動流体での高温と低温の温度差が小さくなる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]の仕事3.9
絶対値を外すと
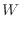 14
14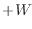 32
[J]
32
[J]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 膨張弁(仕事は取り出さず、粘性消散3.10
流れで渦が発生し徐々に小さな渦となり、粘性により渦の運動エネルギーが熱に変換される
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...で示した熱力学的平衡の熱平衡、力学平衡、相平衡、化学平衡のうち、閉じた系と周囲との間で物質の直接接触や物質の移動がないので、系と周囲の関係で相平衡、化学平衡については考える必要がなく、熱平衡と力学平衡について考える。
3.11
また断熱変化では熱平衡を、等積変化では力学平衡を考える必要がない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]も前後の状態で決まる3.12
準静過程でない場合は仕事が前後の状態で決まらないため、熱量もどの程度の大きさとなるか前後の状態だけでは分からない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
全体として断熱された系において不可逆の指標となる状態量としたい4.1
作用された系、作用した系の両方の変化を含めて可逆・不可逆を考える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...条件2の不可逆の変化で増加する性質を考える。温度差がある物体間で熱が伝わる場合や、熱が発生する場合は現象は不可逆となる
4.2
条件2では断熱された一つの系を考えているので、発熱のみで熱の伝わりを考慮する必要はないが、条件3のために熱の伝わりも考える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...条件3の全体は断熱された系の内部に複数の系があり内部で熱のやり取りのある場合を考える。ここでは内部の系として、高温熱源の系と低温熱源の系4.3
ここで熱源の条件は3.1.2節
 で示したように温度だけである。
で示したように温度だけである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[K]の系へ伝わったときを考える
4.4
微小な熱量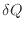 は変化量ではなく完全微分ではないため、不完全微分を表す
は変化量ではなく完全微分ではないため、不完全微分を表す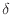 で表す。
で表す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]4.5
高温の系では熱が奪われるので負の値。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]4.6
低温の系では熱が与えられるので正の値。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
上式において、左辺は仕事をされる圧縮過程で正としており、右辺の体積変化は圧縮過程で負4.7
体積が
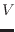 1
から
1
から
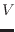 2
に変化するとすると、圧縮では
2
に変化するとすると、圧縮では
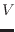 1
1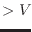 2
である。体積変化は
2
である。体積変化は
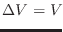 2
2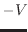 1
1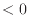 となり負である。
となり負である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...から外すことができる4.8
式中の
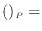 const.
で等圧変化であることを示す。
const.
で等圧変化であることを示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
ここでは、開いた系などの全体として熱力学的平衡が成り立たない、より一般的な系でも、これまでの熱力学の結果を適用できる(温度などを使える)ように、局所熱力学的平衡の概念を導入する。詳細については熱力学の範疇ではないためここでは扱わないので、考え方だけ把握してほしい4.9
興味があれば文献[16][17]や、ボルツマン分布については統計熱力学の参考書を参照するとよい。温度とボルツマン分布についてはAtkinsの本[18]もわかりやすい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
現実的な非平衡な系において、これまでに定義した温度や圧力などを適用するため、局所熱力学的平衡の概念を導入する。局所熱力学的平衡では系を非常に小さくとり局所的には温度や圧力の分布が一様で熱力学的平衡が成り立っていると考える4.10
この局所熱力学的平衡はほとんどの現実的な状況において成り立つと考えられ、統計熱力学的には分子数とエネルギーの関係がボルツマン分布となる。連続体として扱えないような分子数が少ない場合や変化の時間が短い場合は局所熱力学的平衡が成り立たないこともある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...実際に起こる現象は全て不可逆であり、可逆の現象は理想化された現象である。可逆の現象は時間が進んだ場合の変化を逆向きにした場合の変化も起こすことができる
A.1
現象をカメラで動画を撮って、そのまま再生した場合と逆再生をした場合にどちらの映像も実際に起こりうる現象である場合が可逆の現象である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...熱が伝わる現象は必ず不可逆となる。高温の物体と低温の物体を接触させて、2つの物体の温度が近くなる現象を考える。100℃の物体と10℃の物体を10秒間接触させ、90℃と20℃に変化する現象を考える。逆向きの現象を考える場合、運動していないため方向は変化しないA.2
静止していれば動画を逆向きに再生しても方向は変わらない
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Jが取り出される仕事B.1
支持棒へした仕事(取り出せる仕事)
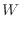 pis
pis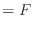 pis
pis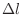 は式(B.1)より次のように表される。
は式(B.1)より次のように表される。
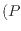 sys
sys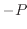 env
env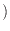 のように、周囲環境と系との圧力差で示した圧力をゲージ圧と呼び多くの圧力計はこのゲージ圧を測定している。このゲージ圧を用いると体積変化
のように、周囲環境と系との圧力差で示した圧力をゲージ圧と呼び多くの圧力計はこのゲージ圧を測定している。このゲージ圧を用いると体積変化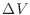 から取り出せる仕事を求めることができる。
から取り出せる仕事を求めることができる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[℃またはK]は任意の有限の温度差とする。例として壁での熱伝導による熱の伝わりを考えると、熱伝導の式(フーリエの法則B.2
詳細は伝熱のテキスト[19][20]を参照すること
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...系の内部での平衡の条件を考える。過程において系の内部で力学平衡となっていない条件として、内部で圧力分布があり流れが起きる状態があげられる。また、内部の流れが徐々に小さな渦となることにより流体の運動エネルギーが熱に変換されることで熱平衡も成り立たなくなる(粘性消散)B.3
熱に変換される(発熱する)ことにより、ある場所での温度が高くなり熱平衡ではなくなる
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
また、ピストンの移動速度によりやりとりする仕事が変化することも考えられるB.4
系の内部分子の速度に対してピストンの速度が速いとき、膨張過程ではピストン壁が遠ざかることから受ける圧力が小さくなり、取り出せる仕事が減る。圧縮過程では壁と分子の相対速度が増加するため必要な仕事が増える。速度としては音速のオーダーであり、圧力波が発生すると思われる。通常、移動速度により変化する仕事の量は測定できないほど小さい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)が成り立っており十分に小さな系を考えれば、実際の現象においても断熱変化は可逆過程となりうる(系の内部で流れによる粘性消散B.5
流れで渦が発生し徐々に小さな渦となり粘性により運動エネルギーが熱に変換される。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
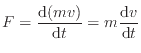
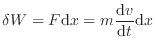
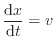 なので、
なので、
![]() [J]が状態0
から状態
[J]が状態0
から状態![]() まで作用するときに、その区間で積分すると、
まで作用するときに、その区間で積分すると、
![$\displaystyle W = \int_0^1 \delta W = \int_0^1 F \mathrm{d}x = \int_0^1 m v \ma...
...m \biggl[\frac{1}{2} v^2 \biggr]_0^1 = \frac{1}{2} mv_1^2 - \frac{1}{2} mv_0^2
$](img38.png)