


Next: 1.2.4 発熱
Up: 1.2 熱力学第一法則
Previous: 1.2.2 熱
1.2.3 内部エネルギー
熱が伝わった際に、系の内部で変化するエネルギーが内部エネルギーである。内部エネルギーには、温度に応じて変化するエネルギーである顕熱と相変化のエネルギーである潜熱が含まれる。伝わった熱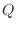 [J]のエネルギーだけ内部エネルギー
[J]のエネルギーだけ内部エネルギー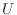 [J]が変化することを式で表すと
[J]が変化することを式で表すと
となる
1.4。
質量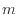 [kg]の物体の温度の微小変化
[kg]の物体の温度の微小変化
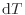 [℃またはK]による内部エネルギーの微小変化量
[℃またはK]による内部エネルギーの微小変化量
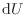 [J](顕熱微小変化量)は、定積比熱
[J](顕熱微小変化量)は、定積比熱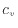 [J/(kg
[J/(kg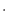 K)]
1.5により次の様に表される。
K)]
1.5により次の様に表される。
温度の変化に対して定積比熱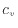 [J/(kg
[J/(kg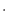 K)]を一定とみなすことが出来れば
1.6、温度変化
K)]を一定とみなすことが出来れば
1.6、温度変化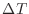 [℃またはK]による内部エネルギーの変化量
[℃またはK]による内部エネルギーの変化量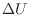 [J]は次式で表される。
[J]は次式で表される。
図1.1のように2つの物体を接触させると、伝わった熱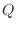 [J]の分だけ、質量
[J]の分だけ、質量
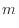 h
[kg]で定積比熱
h
[kg]で定積比熱
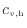 [J/(kg
[J/(kg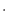 K)]の高温の物体の内部エネルギーは
K)]の高温の物体の内部エネルギーは
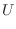 h1
[J]から
h1
[J]から
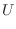 h2
[J]に減少し(
h2
[J]に減少し(
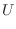 h1
h1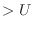 h2
)、質量
h2
)、質量
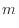 l
[kg]で定積比熱
l
[kg]で定積比熱
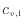 [J/(kg
[J/(kg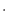 K)]の低温の物体の内部エネルギーは
K)]の低温の物体の内部エネルギーは
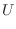 l1
[J]から
l1
[J]から
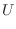 l2
[J]に増加する(
l2
[J]に増加する(
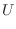 l1
l1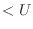 l2
)。この内部エネルギーの変化量に応じて、物体の温度が変化する。高温物体の内部エネルギーの変化(減少)
l2
)。この内部エネルギーの変化量に応じて、物体の温度が変化する。高温物体の内部エネルギーの変化(減少)
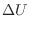 h
[J]は次式より求まる
1.7。
h
[J]は次式より求まる
1.7。
温度の変化に対して定積比熱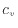 [J/(kg
[J/(kg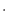 K)]を一定とみなすことが出来れば、次式より求まる。
K)]を一定とみなすことが出来れば、次式より求まる。
低温物体の内部エネルギーの変化(増加)
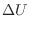 l
[J]も同様に次式より求まる。
l
[J]も同様に次式より求まる。
温度の変化に対して定積比熱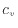 [J/(kg
[J/(kg K)]を一定とみなすことが出来れば、次式より求まる。
K)]を一定とみなすことが出来れば、次式より求まる。
伝わった熱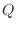 [J]と内部エネルギーの変化
[J]と内部エネルギーの変化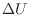 [J]は式(1.1)
[J]は式(1.1)
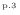 に示すように等しく、また高温の物体の内部エネルギーの変化したエネルギーが熱となって伝わり低温の物体の内部エネルギーを上昇させるため、高温の物体と低温の物体の内部エネルギーの変化量の絶対値は等しく次の関係が成り立つ
1.8。
に示すように等しく、また高温の物体の内部エネルギーの変化したエネルギーが熱となって伝わり低温の物体の内部エネルギーを上昇させるため、高温の物体と低温の物体の内部エネルギーの変化量の絶対値は等しく次の関係が成り立つ
1.8。
このように内部エネルギーは系の持っているエネルギーであり、熱は物体間に温度差がある場合ある物体から別の物体へと伝わるエネルギーである。熱の移動は温度の差がある場合に起こり、物質や大きさが違えば温度が同じでも内部エネルギーが違うこともありえるが、内部エネルギーの差では熱の移動は起こらない。また温度の低い物体から温度の高い物体へ熱は伝わらないため、熱が伝わる現象は不可逆である。可逆と不可逆の詳細については付録A.1
 に示す。
に示す。



Next: 1.2.4 発熱
Up: 1.2 熱力学第一法則
Previous: 1.2.2 熱
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() [J]の分だけ、質量
[J]の分だけ、質量
![]() h
[kg]で定積比熱
h
[kg]で定積比熱
![]() [J/(kg
[J/(kg![]() K)]の高温の物体の内部エネルギーは
K)]の高温の物体の内部エネルギーは
![]() h1
[J]から
h1
[J]から
![]() h2
[J]に減少し(
h2
[J]に減少し(
![]() h1
h1![]() h2
)、質量
h2
)、質量
![]() l
[kg]で定積比熱
l
[kg]で定積比熱
![]() [J/(kg
[J/(kg![]() K)]の低温の物体の内部エネルギーは
K)]の低温の物体の内部エネルギーは
![]() l1
[J]から
l1
[J]から
![]() l2
[J]に増加する(
l2
[J]に増加する(
![]() l1
l1![]() l2
)。この内部エネルギーの変化量に応じて、物体の温度が変化する。高温物体の内部エネルギーの変化(減少)
l2
)。この内部エネルギーの変化量に応じて、物体の温度が変化する。高温物体の内部エネルギーの変化(減少)
![]() h
[J]は次式より求まる
1.7。
h
[J]は次式より求まる
1.7。
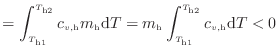
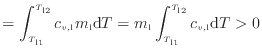
![]() [J]と内部エネルギーの変化
[J]と内部エネルギーの変化![]() [J]は式(1.1)
[J]は式(1.1)
![]() に示すように等しく、また高温の物体の内部エネルギーの変化したエネルギーが熱となって伝わり低温の物体の内部エネルギーを上昇させるため、高温の物体と低温の物体の内部エネルギーの変化量の絶対値は等しく次の関係が成り立つ
1.8。
に示すように等しく、また高温の物体の内部エネルギーの変化したエネルギーが熱となって伝わり低温の物体の内部エネルギーを上昇させるため、高温の物体と低温の物体の内部エネルギーの変化量の絶対値は等しく次の関係が成り立つ
1.8。
![]() に示す。
に示す。