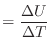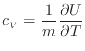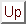


Next: 1.2.7 熱の伝わりによる内部エネルギーの変化
Up: 1.2 熱力学第一法則
Previous: 1.2.5 熱力学第一法則の式
1.2.6 温度と内部エネルギー
ここでは内部エネルギーと温度の関係を述べる。この関係がなくても熱力学を展開していくことが出来るが、内部エネルギーのイメージをつけてもらうためにここで説明する。
仕事や熱が伝わった際に、系の内部で変化するエネルギーが内部エネルギーである。内部エネルギーには、温度に応じて変化するエネルギーである顕熱と相変化のエネルギーである潜熱が含まれる。
蒸発や融解などの相変化のない単相から成り立つ系では熱を受け取り内部エネルギーが増えると温度が上昇する。熱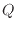 [J]
のみを受け取り仕事の作用がない系の体積が一定である条件での、内部エネルギーの変化量
[J]
のみを受け取り仕事の作用がない系の体積が一定である条件での、内部エネルギーの変化量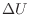 [J]
と温度の変化量
[J]
と温度の変化量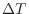 [K]
の関係を等積熱容量
[K]
の関係を等積熱容量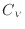 [J/K]
で次のように表される。
[J/K]
で次のように表される。
通常、この等積熱容量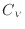 [J/K]
は温度によって変化するので、
[J/K]
は温度によって変化するので、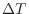 の温度変化でも値が変わる。ある温度での値を求めるために、
の温度変化でも値が変わる。ある温度での値を求めるために、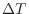 のゼロの極限を取り偏微分の形で次のように表す。
のゼロの極限を取り偏微分の形で次のように表す。
また、系の質量を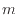 [kg]
とし上式(1.6)の両辺を質量
[kg]
とし上式(1.6)の両辺を質量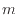 [kg]
で割ることで、質量あたりの内部エネルギーの変化を表す等積比熱
[kg]
で割ることで、質量あたりの内部エネルギーの変化を表す等積比熱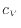 [J/(kg K)]
を次式のように表すことが出来る
1.6。
[J/(kg K)]
を次式のように表すことが出来る
1.6。
定積比熱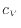 [J/(kg K)]
は物質の状態が決まれば値が決まる物性値である。温度の変化に対する変化が十分に小さく一定とみなすことが出来れば
1.7、温度変化
[J/(kg K)]
は物質の状態が決まれば値が決まる物性値である。温度の変化に対する変化が十分に小さく一定とみなすことが出来れば
1.7、温度変化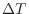 [℃またはK]
による内部エネルギーの変化量
[℃またはK]
による内部エネルギーの変化量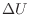 [J]
は次式で表される。
[J]
は次式で表される。



Next: 1.2.7 熱の伝わりによる内部エネルギーの変化
Up: 1.2 熱力学第一法則
Previous: 1.2.5 熱力学第一法則の式
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。
![]() [J]
のみを受け取り仕事の作用がない系の体積が一定である条件での、内部エネルギーの変化量
[J]
のみを受け取り仕事の作用がない系の体積が一定である条件での、内部エネルギーの変化量![]() [J]
と温度の変化量
[J]
と温度の変化量![]() [K]
の関係を等積熱容量
[K]
の関係を等積熱容量![]() [J/K]
で次のように表される。
[J/K]
で次のように表される。