1.2.10 解答

学問 -top-

Next: 1.3 熱力学第二法則 Up: 1.2 熱力学第一法則 Previous: 1.2.9 問題

1.2.10 解答

熱、単位はJ（ジュール）。1.2.3節 $^{\text{p.\pageref{sec-Heat}}}$ 参照。
内部エネルギー、単位はJ（ジュール）。1.2.6節 $^{\text{p.\pageref{sec-InternalEnergy}}}$ 参照。
作用するエネルギーは熱・仕事、系が保有するエネルギーは内部エネルギー・運動エネルギー・位置エネルギー。すべて単位はJ（ジュール）。参考までに他の単位は運動量[kg m/s]・温度[℃またはK]・圧力[Pa]・速度[m/s]である。
机から跳び、床に降りることで、机と床での位置エネルギーの差、跳んだ速度と床で止まった状態との運動エネルギーの差は、熱となって床または部屋の空気に伝わり内部エネルギーが変化する。この問題では全て空気に伝わるとしている。位置エネルギーの変化量 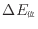$\Delta E_\mathrm{位}$ と運動エネルギーの変化量 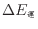$\Delta E_\mathrm{運}$ を求める。
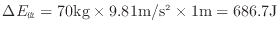
$\Delta E_\mathrm{位} = 70 {\rm kg} \times 9.81 {\rm m/s^2} \times 1 {\rm m} = 686.7 {\rm J}$
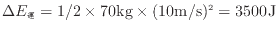
$\Delta E_\mathrm{運} = 1 / 2 \times 70 {\rm kg} \times (10 {\rm m/s})^2 = 3500 {\rm J}$
位置エネルギーと運動エネルギーの変化量の合計の4186.7 J空気の内部エネルギーが変化する。次に6畳の部屋の体積を求める。
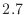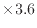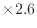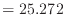m $\times 3.6$ m $\times 2.6$ m m
空気の密度は1.176 kg/m とあるので、部屋の空気の質量を求める。
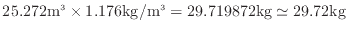
$25.272 {\rm m^3} \times 1.176 {\rm kg/m^3} = 29.719872 {\rm kg} \simeq 29.72 {\rm kg}$
式(1.7) $^{\text{p.\pageref{eq-InternalTemperatureDelta}}}$ を変形し温度変化を求める。内部エネルギーの変化量を部屋の空気の質量と比熱で割る。
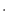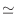4186.7 J / {0.717 kJ/(kg $\cdot$ K) $\times$ 29.72 kg} $\simeq$ 0.196 K
部屋の温度が約0.2 K（℃）上昇する。
問4から6畳の部屋の体積は25.272 m 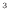、部屋の空気の質量は29.72kgである。式(1.7) $^{\text{p.\pageref{eq-InternalTemperatureDelta}}}$ より内部エネルギーの変化が求まる。
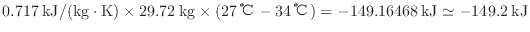
$0.717 \: {\rm kJ/(kg \cdot K)} \times 29.72 \: {\rm kg} \times ( 27 \: {\rm ℃} - 34 \: {\rm ℃} ) = - 149.16468 \: {\rm kJ} \simeq - 149.2 \: {\rm kJ}$
内部エネルギーの変化量と同じエネルギーを熱として奪う（式(1.10) $^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ ）ので、熱の大きさは- 149.2 kJである。
鍋の中の水の質量を求める。
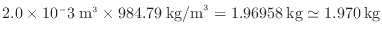
$2.0 \times 10^-3 \: {\rm m}^3 \times 984.79 \: {\rm kg/m}^3 = 1.96958 \: {\rm kg} \simeq 1.970 \: {\rm kg}$
式(1.7) $^{\text{p.\pageref{eq-InternalTemperatureDelta}}}$ より内部エネルギーの変化が求まる。
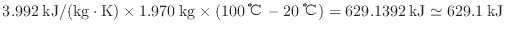
$3.992 \: {\rm kJ/(kg \cdot K)} \times 1.970 \: {\rm kg} \times ( 100 \: {\rm ℃} - 20 \: {\rm ℃} ) = 629.1392 \: {\rm kJ} \simeq 629.1 \: {\rm kJ}$
内部エネルギーの変化量と同じエネルギーを加熱する（式(1.10) 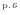$^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ ）ので、熱の大きさは629.1 kJである。
問4から6畳の部屋の体積は25.272 m 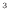、部屋の空気の質量は29.72kgである。また、問5から鍋の中の水の質量は1.97kgである。等しくなった際の温度を 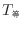$T_\mathrm{等}$ とすると、お湯の内部エネルギーの変化 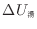$\Delta U_\mathrm{湯}$ と部屋の空気の内部エネルギーの変化 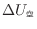$\Delta U_\mathrm{空}$ は式(1.7) 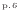$^{\text{p.\pageref{eq-InternalTemperatureDelta}}}$ より次式で表される。
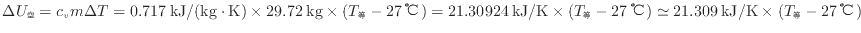
$\Delta U_\mathrm{空} = c_{v} m \Delta T = 0.717 \: {\rm kJ/(kg \cdot K)} \tim... ...℃} ) \simeq 21.309 \: {\rm kJ/K} \times ( T_\mathrm{等} - 27 \: {\rm ℃} )$
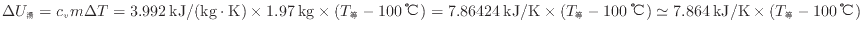
$\Delta U_\mathrm{湯} = c_{v} m \Delta T = 3.992 \: {\rm kJ/(kg \cdot K)} \tim... ...℃} ) \simeq 7.864 \: {\rm kJ/K} \times ( T_\mathrm{等} - 100 \: {\rm ℃} )$
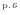内部エネルギーの変化は等しい（式(1.10) $^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ ）ので次式が成り立つ。
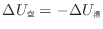
$\Delta U_\mathrm{空} = - \Delta U_\mathrm{湯}$
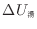上式に $\Delta U_\mathrm{空}$ 、 $\Delta U_\mathrm{湯}$ の値を代入すると次の関係が成り立つ。
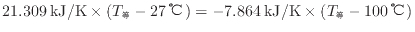
$21.309 \: {\rm kJ/K} \times ( T_\mathrm{等} - 27 \: {\rm ℃} ) = - 7.864 \: {\rm kJ/K} \times ( T_\mathrm{等} - 100 \: {\rm ℃} )$
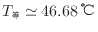
$T_\mathrm{等} \simeq 46.68 \: {\rm ℃}$
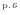また、内部エネルギーの変化と伝わった熱の大きさは等しい（式(1.10) $^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ ）ので次式が成り立つ。
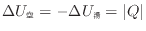
$\Delta U_\mathrm{空} = - \Delta U_\mathrm{湯} = \vert Q\vert$
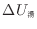$\Delta U_\mathrm{湯}$ から伝わった熱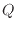を求める。
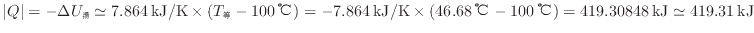
$\vert Q\vert = - \Delta U_\mathrm{湯} \simeq 7.864 \: {\rm kJ/K} \times ( T_\... ...\rm ℃} - 100 \: {\rm ℃} ) = 419.30848 \: {\rm kJ} \simeq 419.31 \: {\rm kJ}$
2 Lのお湯で6畳の部屋を46.68℃まで温めることができ、伝わる熱の大きさは419.31 kJである。
お湯の質量を求める。
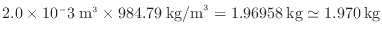
$2.0 \times 10^-3 \: {\rm m}^3 \times 984.79 \: {\rm kg/m}^3 = 1.96958 \: {\rm kg} \simeq 1.970 \: {\rm kg}$
等しくなった際の温度を 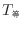$T_\mathrm{等}$ とすると、お湯の内部エネルギーの変化 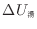$\Delta U_\mathrm{湯}$ とレトルトカレーの内部エネルギーの変化 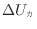$\Delta U_\mathrm{カ}$ は式(1.7) 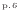$^{\text{p.\pageref{eq-InternalTemperatureDelta}}}$ より次式で表される。
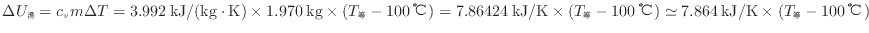
$\Delta U_\mathrm{湯} = c_{v} m \Delta T = 3.992 \: {\rm kJ/(kg \cdot K)} \tim... ...℃} ) \simeq 7.864 \: {\rm kJ/K} \times ( T_\mathrm{等} - 100 \: {\rm ℃} )$
$\Delta U_\mathrm{カ} = c_{v} m \Delta T = 3.992 \: {\rm kJ/(kg \cdot K)} \tim... ... ℃} ) \simeq 0.798 \: {\rm kJ/K} \times ( T_\mathrm{等} - 20 \: {\rm ℃} )$
内部エネルギーの変化は等しい（式(1.10 $^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ )）ので次式が成り立つ。
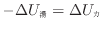
$- \Delta U_\mathrm{湯} = \Delta U_\mathrm{カ}$
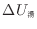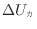上式に $\Delta U_\mathrm{湯}$ 、 $\Delta U_\mathrm{カ}$ の値を代入すると次の関係が成り立つ。
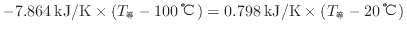
$- 7.864 \: {\rm kJ/K} \times ( T_\mathrm{等} - 100 \: {\rm ℃} ) = 0.798 \: {\rm kJ/K} \times ( T_\mathrm{等} - 20 \: {\rm ℃} )$
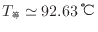
$T_\mathrm{等} \simeq 92.63 \: {\rm ℃}$
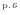また、内部エネルギーの変化と伝わった熱の大きさは等しい（式(1.10) $^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ ）ので次式が成り立つ。
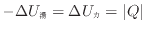
$- \Delta U_\mathrm{湯} = \Delta U_\mathrm{カ} = \vert Q\vert$
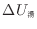$\Delta U_\mathrm{湯}$ から伝わった熱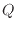を求める。
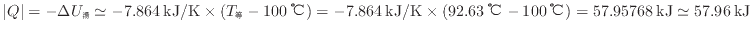
$\vert Q\vert = - \Delta U_\mathrm{湯} \simeq - 7.864 \: {\rm kJ/K} \times ( T... ... {\rm ℃} - 100 \: {\rm ℃} ) = 57.95768 \: {\rm kJ} \simeq 57.96 \: {\rm kJ}$
2 Lのお湯でレトルトカレーを92.63 ℃まで温めることができ、伝わる熱の大きさは57.96 kJである。
快適と考える温度を18℃として解答をする。また、18℃となる鍋の中のお湯の質量を 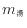$m_\mathrm{湯}$ とおく。問4から6畳の部屋の体積は25.272 m 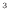、部屋の空気の質量は29.72kgである。部屋の空気の内部エネルギーの変化 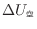$\Delta U_\mathrm{空}$ とお湯の内部エネルギーの変化 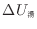$\Delta U_\mathrm{湯}$ は式(1.7) 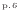$^{\text{p.\pageref{eq-InternalTemperatureDelta}}}$ より次式で表される。
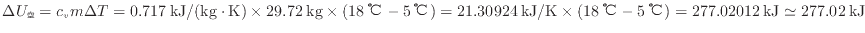
$\Delta U_\mathrm{空} = c_{v} m \Delta T = 0.717 \: {\rm kJ/(kg \cdot K)} \tim... ...{\rm ℃} - 5 \: {\rm ℃} ) = 277.02012 \: {\rm kJ} \simeq 277.02 \: {\rm kJ}$
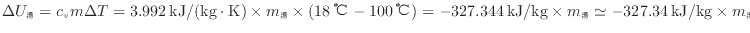
$\Delta U_\mathrm{湯} = c_{v} m \Delta T = 3.992 \: {\rm kJ/(kg \cdot K)} \tim... ...kg} \times m_\mathrm{湯} \simeq - 327.34 \: {\rm kJ/kg} \times m_\mathrm{湯}$
内部エネルギーの変化は等しい（式(1.10) 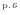$^{\text{p.\pageref{eq-HeatInternalHighLow}}}$ ）ので次式が成り立つ。
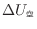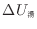$\Delta U_\mathrm{空} = - \Delta U_\mathrm{湯}$
上式に $\Delta U_\mathrm{空}$ 、 $\Delta U_\mathrm{湯}$ の値を代入すると次の関係が成り立つ。
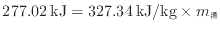
$277.02 \: {\rm kJ} = 327.34 \: {\rm kJ/kg} \times m_\mathrm{湯}$
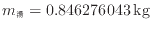
$m_\mathrm{湯} = 0.846276043 \: {\rm kg}$
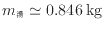
$m_\mathrm{湯} \simeq 0.846 \: {\rm kg}$
問5よりお湯の密度は984.79 kg/m であるので体積は以下のように求まる。
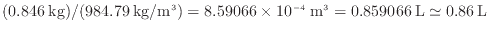
$(0.846 \: {\rm kg}) / (984.79 \: {\rm kg/m^3}) = 8.59066 \times 10^{-4} \: {\rm m}^3 = 0.859066 \: \rm L \simeq 0.86 \: \rm L$
0.86 Lの100℃のお湯で6畳の部屋を5℃から18℃に暖めることができる。