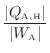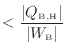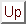


Next: 1.4.6 可逆熱機関(可逆ヒートポンプ)での熱の比
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.4 可逆熱機関(可逆ヒートポンプ)の効率
1.4.5 可逆と不可逆の熱機関(ヒートポンプ)での効率の比較
ここでは可逆熱機関(可逆ヒートポンプ)の効率が不可逆熱機関や不可逆ヒートポンプの効率よりも低い場合には熱力学第二法則に反することを示し、可逆熱機関(可逆ヒートポンプ)の効率は不可逆熱機関や不可逆ヒートポンプの効率よりも必ず高くなることを示す。
まず可逆熱機関と不可逆熱機関の比較をする。不可逆熱機関Aと可逆熱機関Bを考える。ここで、不可逆熱機関Aの効率
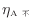 が可逆熱機関Bの効率
が可逆熱機関Bの効率
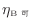 よりも高いと仮定しよう(図1.8-1)。
よりも高いと仮定しよう(図1.8-1)。
効率の関係の式(1.13)
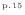 から、次式が成り立つ。
から、次式が成り立つ。
可逆熱機関Bは可逆でありヒートポンプとしても動作できる(図1.8-2)ので、不可逆熱機関Aが周囲に受け渡す仕事と同じだけ仕事を受け取る(
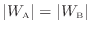 )可逆ヒートポンプとして動作させる(図1.8-3)と次式が成り立つ。
)可逆ヒートポンプとして動作させる(図1.8-3)と次式が成り立つ。
エネルギーの保存式(1.12)と式(1.15)と、仕事の大きさの関係(
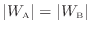 )から、
)から、
となり、図1.8-4のように周囲になにも変化を残さず、低温熱源から(
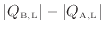 )[J]または(
)[J]または(
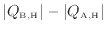 )[J]を高温熱源へ伝えることが出来てしまう。よって可逆熱機関よりも効率の良い不可逆熱機関は熱力学第二法則クラウジウスの原理(1.3節
)[J]を高温熱源へ伝えることが出来てしまう。よって可逆熱機関よりも効率の良い不可逆熱機関は熱力学第二法則クラウジウスの原理(1.3節
 )に反する。このことから可逆熱機関の効率が必ず高くなるといえる。
)に反する。このことから可逆熱機関の効率が必ず高くなるといえる。
不可逆熱機関Aの効率
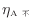 が可逆熱機関Bの効率
が可逆熱機関Bの効率
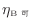 よりも低い場合には熱力学第二法則に反することはない(付録A.4
よりも低い場合には熱力学第二法則に反することはない(付録A.4
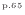 参照)。
参照)。
不可逆ヒートポンプBと可逆ヒートポンプAを比較する。ここで、不可逆ヒートポンプBの成績係数が可逆ヒートポンプAの効率よりも高いと仮定する(図1.9-1)。
式(1.16)
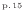 より次式が成り立つ。
より次式が成り立つ。
可逆ヒートポンプAは可逆であり熱機関としても動作できる(図1.9-2)ので、不可逆ヒートポンプBと同じ大きさの仕事で(
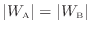 )熱機関として動作させる(図1.9-3)と次式が成り立つ。
)熱機関として動作させる(図1.9-3)と次式が成り立つ。
この場合も先ほどと同様、周囲になにも変化を残さず、低温熱源から
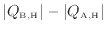 ( =
( =
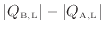 )を高温熱源へ伝えることが出来てしまう(図1.9-4)。よって可逆ヒートポンプよりも効率の良い不可逆ヒートポンプは熱力学第二法則クラウジウスの原理に反する。
)を高温熱源へ伝えることが出来てしまう(図1.9-4)。よって可逆ヒートポンプよりも効率の良い不可逆ヒートポンプは熱力学第二法則クラウジウスの原理に反する。
図 1.9:
可逆ヒートポンプと不可逆ヒートポンプの比較
|
|
以上のように、熱機関としてもヒートポンプとしても同じ効率で動作できる可逆熱機関(可逆ヒートポンプ)では逆の働きをさせることが出来るため、可逆熱機関や可逆ヒートポンプの効率よりも不可逆熱機関や不可逆ヒートポンプの効率が高いと熱力学の第二法則クラウジウスの原理に反する。このことから、同じ二つの熱源間で動作する可逆熱機関(可逆ヒートポンプ)の効率は必ず不可逆熱機関や不可逆ヒートポンプの効率よりも高くなる
1.16。



Next: 1.4.6 可逆熱機関(可逆ヒートポンプ)での熱の比
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.4 可逆熱機関(可逆ヒートポンプ)の効率
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。
![]() が可逆熱機関Bの効率
が可逆熱機関Bの効率
![]() よりも高いと仮定しよう(図1.8-1)。
よりも高いと仮定しよう(図1.8-1)。
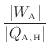
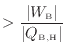
![]() が可逆熱機関Bの効率
が可逆熱機関Bの効率
![]() よりも低い場合には熱力学第二法則に反することはない(付録A.4
よりも低い場合には熱力学第二法則に反することはない(付録A.4
![]() 参照)。
参照)。