• 学問 -top-

1.4.4 可逆熱機関（可逆ヒートポンプ）の効率

ここでは二つの熱源間で動作する可逆熱機関（可逆ヒートポンプ）の効率（仕事と熱の比）が異なる場合には熱力学第二法則に反することから、二つの熱源間で動作する可逆熱機関（可逆ヒートポンプ）の効率はどのような可逆熱機関（可逆ヒートポンプ）でも常に等しくなることを示す。

可逆熱機関（可逆ヒートポンプ）Aと可逆熱機関（可逆ヒートポンプ）Bを並べて同じ二つの熱源間で動作させる。可逆熱機関（可逆ヒートポンプ）Aの熱機関としての効率 $\eta_\mathrm{A}$ [-]が、可逆熱機関（可逆ヒートポンプ）Bの熱機関としての効率 $\eta_\mathrm{B}$ [-]よりも高いと仮定する（図1.6-1）。

$$\eta_\mathrm{A} > \eta_\mathrm{B}$$ (1.18)

効率の高い可逆熱機関（可逆ヒートポンプ）Aを熱機関として、可逆熱機関（可逆ヒートポンプ）Bをヒートポンプとして、仕事の大きさが同じになるように動作させ^1.15（図1.6-2）、熱機関で取り出した仕事でヒートポンプを動作させる（図1.6-3）。

図 1.6: 可逆熱機関（可逆ヒートポンプ）の比較

式(1.13)と式(1.18)から

$$\frac{ \vert W_\mathrm{A} \vert }{ \vert Q_\mathrm{A, H} \vert } > \frac{ \vert W_\mathrm{B} \vert }{ \vert Q_\mathrm{B, H} \vert }$$

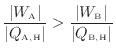
ここで仕事が同じとなるように動作させている（ $\vert W_\mathrm{A} \vert = \vert W_\mathrm{B} \vert$ ）ので、次式が成り立つ。

$$\vert Q_\mathrm{A, H} \vert < \vert Q_\mathrm{B, H} \vert$$ (1.19)

上式と熱機関とヒートポンプにおけるエネルギー保存の式(1.12) $^{\text{p.\pageref{eq-CycleEnergyConservation}}}$ と式(1.15) $^{\text{p.\pageref{eq-CycleEnergyConservationPump}}}$ より、

$$\vert Q_\mathrm{A, L} \vert + \vert W_\mathrm{A} \vert < \vert Q_\mathrm{B, L} \vert + \vert W_\mathrm{B} \vert$$

仕事の大きさが同じになるように動作させている( $\vert W_\mathrm{A} \vert = \vert W_\mathrm{B} \vert$ )ので、次の関係が成り立つ。

$$\vert Q_\mathrm{A, L} \vert < \vert Q_\mathrm{B, L} \vert$$ (1.20)

高温熱源でのやり取りを考えると、式(1.19)より可逆ヒートポンプBの熱 $Q_\mathrm{B, H}$ が大きく（ $\vert Q_\mathrm{B, H} \vert - \vert Q_\mathrm{A, H} \vert > 0$ ）なり、高温熱源へ熱を伝えている。低温熱源では、式(1.20)より可逆ヒートポンプBの熱 $Q_\mathrm{B, L}$ [J]が大きく（ $\vert Q_\mathrm{B, L} \vert - \vert Q_\mathrm{A, L} \vert > 0$ ）なり、低温熱源から熱を伝えている。この可逆熱機関Aと可逆ヒートポンプBでは、仕事は熱機関AからヒートポンプBへするため、周囲との仕事のやりとりはない。可逆熱機関Aと可逆ヒートポンプBをまとめて一つの系と考えれば、この系は熱源との熱のやりとり以外に周囲に何の変化も残しておらず、低温熱源から熱を受けとり、高温熱源へ熱を渡していることになる。これは熱力学第二法則のクラウジウスの原理（1.3節 $^{\text{p.\pageref{sec-2ndLaw}}}$ ）に反する（図1.6-4）。よって、可逆熱機関（可逆ヒートポンプ）Bの熱機関としての効率が可逆熱機関（可逆ヒートポンプ）Aの熱機関としての効率よりも高くなることはありえない。

可逆熱機関（可逆ヒートポンプ）Aの熱機関としての効率が可逆熱機関（可逆ヒートポンプ）Bよりも低いとした場合も、AとBを入れ替えて考え、可逆熱機関（可逆ヒートポンプ）Bを熱機関、可逆熱機関（可逆ヒートポンプ）Aをヒートポンプとして動作させると、同様に低温熱源から高温熱源に熱を伝え、他になにも変化を残さないことになる。よって、同様に熱力学第二法則クラウジウスの原理から、可逆熱機関（可逆ヒートポンプ）Aの熱機関としての効率が可逆熱機関（可逆ヒートポンプ）Bの熱機関としての効率よりも高くなることはありえない。

同じ効率であれば、図1.7ように可逆熱機関Aと可逆ヒートポンプBの熱源とやり取りする熱の量が等しく、全体として熱の移動がないと見なせるため熱力学第二法則に反しない。よって、同じ二つの熱源で動作する可逆熱機関（可逆ヒートポンプ）は必ず同じ効率となる。

図 1.7: 効率の等しい可逆熱機関（可逆ヒートポンプ）

• 学問 -top-

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。