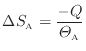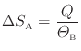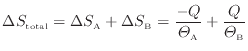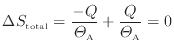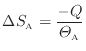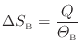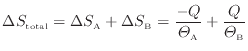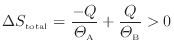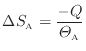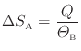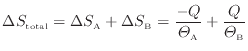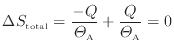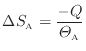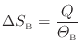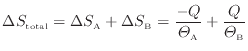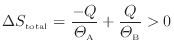


Next: 4.3 エンタルピー
Up: 4.2 エントロピー
Previous: 4.2.3 問題
- 断熱された可逆過程(準静過程)でエントロピーは変化しない(式(4.2)
 )。加熱では増加、冷却では減少する(式(4.3)
)。加熱では増加、冷却では減少する(式(4.3)
 、式(4.5)
、式(4.5)
 )。理想的でない(可逆(準静)でない)過程は不可逆であるので熱を伴いエントロピーは増加する。サイクルでは一周で同じ状態に戻るので変化しない(式(4.4)
)。理想的でない(可逆(準静)でない)過程は不可逆であるので熱を伴いエントロピーは増加する。サイクルでは一周で同じ状態に戻るので変化しない(式(4.4)
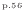 )。
よってそれぞれ次のように変化する。断熱過程
)。
よってそれぞれ次のように変化する。断熱過程
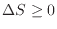 、準静断熱過程
、準静断熱過程
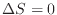 、加熱過程
、加熱過程
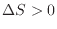 、冷却過程
、冷却過程
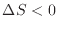 、準静等温加熱過程
、準静等温加熱過程
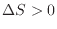 、圧縮過程
、圧縮過程
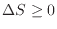 、可逆圧縮過程
、可逆圧縮過程
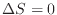 、膨張過程
、膨張過程
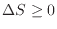 、熱機関サイクル一周
、熱機関サイクル一周
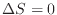 、ヒートポンプサイクル一周
、ヒートポンプサイクル一周
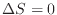 。
。
- エントロピーの変化は式(4.6)
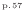 により表されるので熱が奪われる物体Aのエントロピー変化
により表されるので熱が奪われる物体Aのエントロピー変化
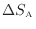 は次式で表される。
は次式で表される。
熱が与えられる物体Bでは次式となる。
全体のエントロピーの変化
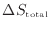 は物体Aと物体Bの変化を足せばよいので次式となる。
は物体Aと物体Bの変化を足せばよいので次式となる。
ここで準静等温過程では熱が伝わる物体間には温度差がないので
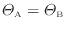 となる。上式に代入すると次式が得られる。
となる。上式に代入すると次式が得られる。
以上のように、可逆過程である準静等温過程では全体のエントロピーは変化しない。
- 前問と同様にエントロピーの変化は式(4.6)
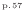 により表されるので熱が奪われる物体Aのエントロピー変化
により表されるので熱が奪われる物体Aのエントロピー変化
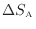 は次式で表される。
は次式で表される。
熱が与えられる物体Bでは次式となる。
全体のエントロピーの変化
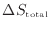 は物体Aと物体Bの変化を足せばよいので次式となる。
は物体Aと物体Bの変化を足せばよいので次式となる。
ここで、熱は温度の高い物体から低い物体に伝わるので
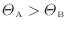 となる。このことと上式より次の関係が成り立つ。
となる。このことと上式より次の関係が成り立つ。
以上のように、通常の熱が伝わる不可逆過程では全体のエントロピーは増加する。



Next: 4.3 エンタルピー
Up: 4.2 エントロピー
Previous: 4.2.3 問題
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。