


Next: B.1.4 熱も状態量ではない
Up: B.1 仕事が状態量ではないのは何故か
Previous: B.1.2 具体的な例
前節のような単純な過程の組み合わせで経路が成り立っていない場合には経路全体を積分し仕事を求める。積分するには経路を指定した経路積分が必要であり、計算の際には媒介変数が用いられる。
媒介変数として時間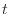 [s]
を取り具体的な計算をしてみる。
体積
[s]
を取り具体的な計算をしてみる。
体積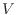 は次式のように初め3.0
は次式のように初め3.0  10
10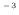 m
m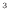 (3.0 リットル)で1 s毎に0.1
(3.0 リットル)で1 s毎に0.1 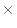 10
10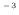 m
m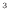 圧縮される。
圧縮される。
圧力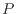 は1.0
は1.0  10
10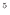 Pa(約一気圧)から次式のように増えていくとする。
Pa(約一気圧)から次式のように増えていくとする。
式(![[*]](crossref.png) )に示すように
)に示すように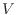 は
は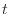 のみの一変数関数として表されている。
のみの一変数関数として表されている。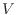 の
の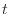 での微分を求める。
での微分を求める。
仕事の微小量を求める式(![[*]](crossref.png) )に式(
)に式(![[*]](crossref.png) )と式(
)と式(![[*]](crossref.png) )を代入して0 sから
)を代入して0 sから
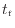 まで経路積分をする。経路中にされた仕事を求めたいので、0 sでの仕事は0 Jである。
まで経路積分をする。経路中にされた仕事を求めたいので、0 sでの仕事は0 Jである。
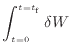 |
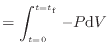 |
|
| |
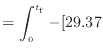 m m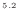 Pa
Pa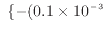 m m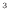 /s
/s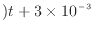 m m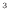
![$\displaystyle \}^{-1.4} ] (- 0.1$](img545.png) m m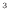 /s
/s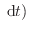 |
|
| |
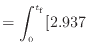 m m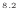 Pa/s
Pa/s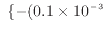 m m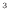 /s
/s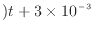 m m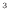
![$\displaystyle \}^{-1.4} ]$](img549.png) m m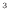 /s
/s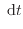 |
|
| |
![$\displaystyle = \left[ \frac{2.937 \text{ m$^{8.2}$\ Pa/s}}{(-0.1)(-0.4)} \{-(0...
...{ m$^3$/s})t + 3 \times 10^{-3} \text{ m$^3$}\}^{-0.4} \right]^{t_\mathrm{f}}_0$](img550.png) |
|
| |
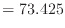 m m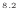 Pa/s
Pa/s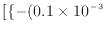 m m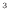 /s
/s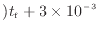 m m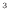
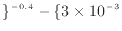 m m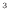
![$\displaystyle \}^{-0.4}]$](img555.png) |
|
| |
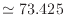 m m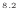 Pa/s
Pa/s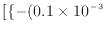 m m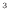 /s
/s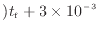 m m
![$\displaystyle \}^{-0.4} - 10.21]$](img557.png) |
|
この変化を前節と同じように図![[*]](crossref.png) に表す。状態の変化に対して仕事が線で表される。
に表す。状態の変化に対して仕事が線で表される。



Next: B.1.4 熱も状態量ではない
Up: B.1 仕事が状態量ではないのは何故か
Previous: B.1.2 具体的な例
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。
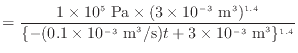
![[*]](crossref.png) )に示すように
)に示すように![[*]](crossref.png) )に式(
)に式(![[*]](crossref.png) )と式(
)と式(![[*]](crossref.png) )を代入して0 sから
)を代入して0 sから
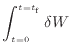
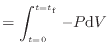
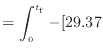 m
m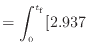 m
m![$\displaystyle = \left[ \frac{2.937 \text{ m$^{8.2}$\ Pa/s}}{(-0.1)(-0.4)} \{-(0...
...{ m$^3$/s})t + 3 \times 10^{-3} \text{ m$^3$}\}^{-0.4} \right]^{t_\mathrm{f}}_0$](img550.png)
![[*]](crossref.png) に表す。状態の変化に対して仕事が線で表される。
に表す。状態の変化に対して仕事が線で表される。