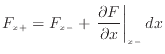


Next: 2.2 質量保存
Up: 2.1 保存量
Previous: 2.1.6 出入の項 拡散
2.1.7 微小項の取り扱い
コントロールボリュームの体積あたりの微小量(
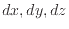 )は十分に小さく無視できると考える。微小体積のコントロールボリュームを考えている(2.1.2節)ため、体積は
)は十分に小さく無視できると考える。微小体積のコントロールボリュームを考えている(2.1.2節)ため、体積は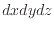 で表される。よって式中では体積あたりの値における微少量(
で表される。よって式中では体積あたりの値における微少量(
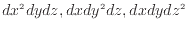 )は十分に小さいとして無視する。
)は十分に小さいとして無視する。
また、項が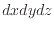 で括られている、または式全体を
で括られている、または式全体を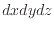 で割った場合には、各境界面での変数の値の差は微小量であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.9)で表されるx軸に垂直な面の左側と右側での差を考える。式(2.9)よりx軸に垂直な面の左側と右側での変数
で割った場合には、各境界面での変数の値の差は微小量であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.9)で表されるx軸に垂直な面の左側と右側での差を考える。式(2.9)よりx軸に垂直な面の左側と右側での変数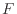 の関係は以下のようになる。
の関係は以下のようになる。
これがコントロールボリュームの体積あたりの値(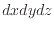 で割った式)であるとすれば、右辺第二項は微小量であるので、無視し、次式のようにx軸左側と右側の値が等しくなり、下付をつけないコントロールボリュームの代表値として表される。
で割った式)であるとすれば、右辺第二項は微小量であるので、無視し、次式のようにx軸左側と右側の値が等しくなり、下付をつけないコントロールボリュームの代表値として表される。



Next: 2.2 質量保存
Up: 2.1 保存量
Previous: 2.1.6 出入の項 拡散
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() で括られている、または式全体を
で括られている、または式全体を![]() で割った場合には、各境界面での変数の値の差は微小量であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.9)で表されるx軸に垂直な面の左側と右側での差を考える。式(2.9)よりx軸に垂直な面の左側と右側での変数
で割った場合には、各境界面での変数の値の差は微小量であるため、各境界面の違いは無視し、下付をつけない。例えば、式(2.9)で表されるx軸に垂直な面の左側と右側での差を考える。式(2.9)よりx軸に垂直な面の左側と右側での変数![]() の関係は以下のようになる。
の関係は以下のようになる。