• 学問 -top-

2.1.4 出入の項 差の計算

境界面でのコントロールボリュームへの出入は、コントロールボリュームを流体内にとった場合、流出入する流体によって運ばれる対流と、分子運動により運ばれる拡散、その他の作用する現象に分けられ、以下のように表せる。

$$時間あたりにコントロールボリュームに出入する物理量 \hspace{5em}$$

$$\hspace{5em} = 対流による出入 + 拡散による出入 + その他の出入$$

このコントロールボリュームで時間あたりにコントロールボリューム内で生成される物理量を生成量と書けば、式(2.1)は

$$\frac{\partial 持っている物理量}{\partial t} = 対流による出入 + 拡散による出入 + その他の出入 + 生成量$$ (2.7)

と書ける。上式のようにコントロールボリューム内の物理量が増えると正となるので出入は“入る量 - 出る量”で計算される。

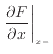この式中の出入の量の求め方を考える。図2.1の左側のyz面で、物理量の出入$F_{x -}$ があるとする。このときの、右のyz面での出入を考える。yz面を通過する出入の量は$x$ の位置によって異なり、$F$ はxの関数である。コントロールボリューム左側から右側に$x$ 方向の位置が$dx$ だけ変わるとき、それぞれでの出入の量、$F_{x -}$ と$F_{x +}$ の値はどう違うだろうか。図2.3に示すように、左側の面での流量$F$ の$x$ 方向への変化量（傾き）は、$x$ で微分した値、 $\left. \dfrac{\partial F}{\partial x} \right\vert _{x -}$ となる。図2.3のグラフのように傾きは 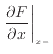$\left. \dfrac{\partial F}{\partial x} \right\vert _{x -}$ であるので、dx離れた右側の位置での縦軸の$F$ の微小変化量$d F$ は、傾きに$dx$ をかけた $\left. 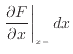\dfrac{\partial F}{\partial x} \right\vert _{x -}dx$ となる。よって、右側の面での出入の量、$F_{x +}$ は次のように表される。

$$F_{x +}= F_{x -}+ d F = F_{x -}+ \left. \frac{\partial F}{\partial x} \right\vert _{x -}dx$$ (2.8)

x方向のyz面における出入の量は、これらの左側の面での$F_{x -}$ と右側の面での$F_{x +}$ から求められる。左側と右側の面では、コントロールボリュームに対して、出る方向と入る方向が逆になるので、差をとると、コントロールボリュームでのx方向の出入の量となる。例えば左から右、xの正の方向に物理量が移っている場合は、左の面では入る方向で増加するプラス、右の面では出て行き減少しマイナスとなる。式で表すと、

$$F_{x -}- F_{x +} = F_{x -}- \bigg( F_{x -}+ \left. \frac{\partial F}{\partial x} \right\vert _{x -}dx \bigg)$$

$$= - \left. \frac{\partial F}{\partial x} \right\vert _{x -}dx$$ (2.9)

となる。式(2.8)の“対流による出入”、“拡散による出入”、“その他の出入”の項は上式(2.10)で表される。入ってくる物理量はベクトルで表され、ベクトルの変化は発散^2.1で表される。

図 2.3: Diffusion

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。