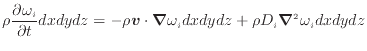


Next: 2.6 一般形
Up: 2.5.4 成分の質量保存式
Previous: 2.5.4.1 圧縮性流体(密度 [kg/m ]は変化する)
成分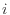 の質量の保存式は、式(2.187)、式(2.207)、式(2.227)より
の質量の保存式は、式(2.187)、式(2.207)、式(2.227)より
両辺を
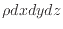 で割って、
で割って、



Next: 2.6 一般形
Up: 2.5.4 成分の質量保存式
Previous: 2.5.4.1 圧縮性流体(密度 [kg/m ]は変化する)
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() の質量の保存式は、式(2.187)、式(2.207)、式(2.227)より
の質量の保存式は、式(2.187)、式(2.207)、式(2.227)より