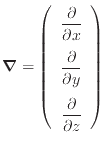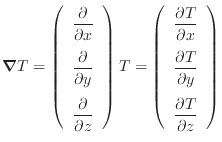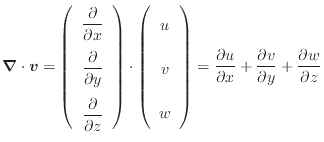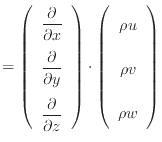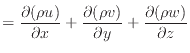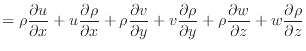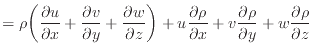


Next: A.2 エネルギー保存式での計算の詳細
Up: A.1 微分
Previous: A.1.2 微分の計算
 (ナブラ)はベクトルで次式で表される。
(ナブラ)はベクトルで次式で表される。
スカラーとの積、例えば温度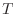 との積は次式のようになる。
との積は次式のようになる。
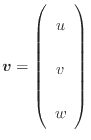
ベクトルとの積(内積)、例えば速度ベクトル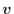 との積は次のようになる。ベクトルの内積なので、積はスカラー量となる。先に速度ベクトル
との積は次のようになる。ベクトルの内積なので、積はスカラー量となる。先に速度ベクトル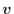 を示す。
を示す。
次にスカラーとベクトルの積との内積、例えばスカラーの密度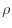 と速度ベクトル
と速度ベクトル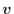 では次のようになる。ベクトルとの内積なので、積はスカラー量となる。
では次のようになる。ベクトルとの内積なので、積はスカラー量となる。
次にスカラー2つとベクトルの積との内積、例えばスカラーの密度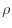 とスカラーの温度
とスカラーの温度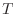 と速度ベクトル
と速度ベクトル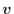 では次のようになる。ベクトルとの内積なので、積はスカラー量となる。
では次のようになる。ベクトルとの内積なので、積はスカラー量となる。



Next: A.2 エネルギー保存式での計算の詳細
Up: A.1 微分
Previous: A.1.2 微分の計算
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。