


Next: 2.1.5 出入の項 面での作用
Up: 2.1 保存量
Previous: 2.1.3 コントロールボリューム
2.1.4 出入の項 対流
対流による出入は“質量流量×質量あたりの物理量”で表される。
この“対流による出入”について考える。対流は移流とも呼ばれ、流体中で流れによって対象とする物理量が運ばれる現象である。例として、図2.3のように水槽の中で、インクの濃度を物理量として考えてみる。水槽の下半分にインクをゆっくり入れ、その後上半分に水をゆっくり注ぐとインクと水はほとんど混ざらず、上部に水、下部にインクの層ができる。この時、水槽の底から上向きの流れを作ったとき(水槽の底にストローが刺さっており、勢いよくインクを入れたとき)インク(濃度の高い流体)が上に向かって流れることにより、インクが水槽下部から上部へ運ばれる。この上向きの流れが発生した位置にコントロールボリュームをとると、下向きの面では対流によりインク(濃度の高い流体)が入り、上向きの面では対流により水(濃度の低い流体)が出て行くことになり、”対流による出入”がおこる。
対流により出入りする量は、対象とする物理量を運ぶ流れの強さによる。例えば図2.2の左側の面から一秒あたりに対象とする物理量が流入する量
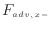 を考える。この
を考える。この
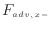 を左側の面に流入する質量流量
を左側の面に流入する質量流量
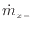 によって表すと、次のようになる。
によって表すと、次のようになる。
ここで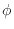 は単位質量あたりの対象とする物理量を表す。インクの例であれば、1kg中に含まれるインクの質量(濃度)が
は単位質量あたりの対象とする物理量を表す。インクの例であれば、1kg中に含まれるインクの質量(濃度)が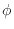 に入る。質量流量
に入る。質量流量
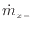 [kg/s]は流体の密度
[kg/s]は流体の密度
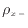 [kg/m
[kg/m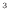 ]と体積流量
]と体積流量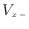 [m
[m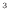 /s]で
/s]で
と表される。また、体積流量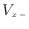 [m
[m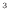 /s]は、通過する図2.2の左側の面
/s]は、通過する図2.2の左側の面
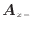 [m
[m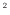 ]の面積が微小(
]の面積が微小(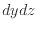 )であるので、速度の分布は一様であるとし、x方向の速度
)であるので、速度の分布は一様であるとし、x方向の速度
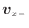 [m/s]2.1と面積
[m/s]2.1と面積
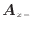 [m
[m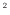 ](速度ベクトルと面積ベクトルの内積)で表される。
](速度ベクトルと面積ベクトルの内積)で表される。
上記三式から、対象とする物理量が流入する量
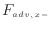 は
は
と表される。



Next: 2.1.5 出入の項 面での作用
Up: 2.1 保存量
Previous: 2.1.3 コントロールボリューム
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![\includegraphics[width=50mm]{figures/Advection.eps}](img68.png)
![]() を考える。この
を考える。この
![]() を左側の面に流入する質量流量
を左側の面に流入する質量流量
![]() によって表すと、次のようになる。
によって表すと、次のようになる。