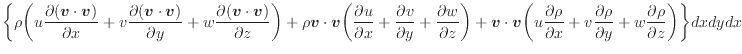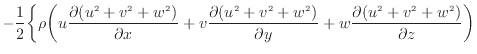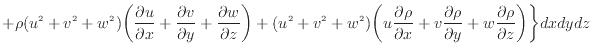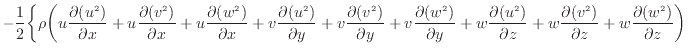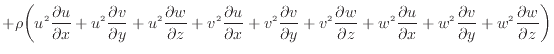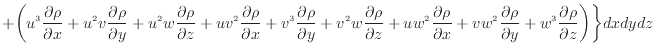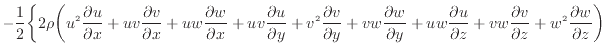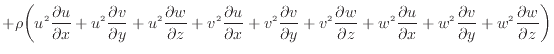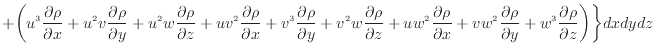... [m/s]2.1
速度ベクトル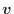 [m/s]はx方向成分速度
[m/s]はx方向成分速度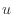 [m/s]、y方向成分速度
[m/s]、y方向成分速度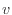 [m/s]、z方向成分速度
[m/s]、z方向成分速度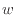 [m/s]で次のように表される。
[m/s]で次のように表される。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の“境界面での作用による出入量”に含まれ、運動量の拡散(粘性2.2
容器の中に粘性係数が高い流体(例えば水飴)と粘性係数が低い流体(例えば空気)で満たしその中で手を動かした時、手が流体に与えた運動量が拡散すると遠くの流体も手と一緒に動き、手は大きな力を感じる。運動量が拡散しづらい流体では近くの流体しか手と一緒に動かないので、手はあまり大きな力を感じない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.../s](運動量では動粘性係数、エネルギーでは熱拡散係数、物質では物質拡散係数)により、次式により表される2.3
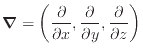
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...は次のように表される2.4
数学的にはテーラー展開から求める(式(A.7)
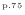 )。
)。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...で表される。入ってくる物理量をベクトルで表すと、変化量は発散2.5
ベクトル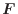 に対する発散は
に対する発散は
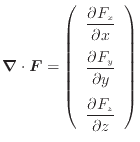 である。
である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.6
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.7
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... [N]として次式のように定義されている2.8
運動量の変化量
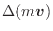 は次式のように、力
は次式のように、力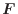 と時間
と時間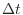 の積で表される力積となる。
の積で表される力積となる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.9
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.10
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...eq-momadvZ)をとり、変形2.11
計算は付録の式(A.2)
 参照
参照
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...eq-press2.12
この式中の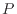 [Pa]は流体力学的圧力である。詳しくは参考文献[1]を参照のこと。
[Pa]は流体力学的圧力である。詳しくは参考文献[1]を参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリューム内を正の方向へ加速させる力を正、負の方向へ加速させる力を負となるように符号を加え、向かい合う面を足し合わせる2.13
コントロールボリュームから出る方向に働く力を正としているので、例えば 軸に垂直な右の面では力が正となる方向でコントロールボリューム内が
軸に垂直な右の面では力が正となる方向でコントロールボリューム内が 軸の正の方向へ加速されるためそのままでよい。しかし、左の面では正の方向で
軸の正の方向へ加速されるためそのままでよい。しかし、左の面では正の方向で 軸の負の方向へ加速され、負の方向で正の方向へ加速されるため負号
軸の負の方向へ加速され、負の方向で正の方向へ加速されるため負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリューム内を正の方向へ加速させる力を正、負の方向へ加速させる力を負となるように符号を加え、向かい合う面を足し合わせる2.14
コントロールボリュームから出る方向に働く力を正としているので、例えば 軸に垂直な右の面では力が正となる方向でコントロールボリューム内が
軸に垂直な右の面では力が正となる方向でコントロールボリューム内が 軸の正の方向へ加速されるためそのままでよい。しかし、左の面では正の方向で
軸の正の方向へ加速されるためそのままでよい。しかし、左の面では正の方向で 軸の負の方向へ加速され、負の方向で正の方向へ加速されるため負号
軸の負の方向へ加速され、負の方向で正の方向へ加速されるため負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.15
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)、下付きを外す。コントロールボリューム全体での対流による運動エネルギーの出入は次式で表される
2.16
式を完全に展開すると以下のようになる。三行目の式から示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.17
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.18
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.19
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.20
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)、下付きを外す。コントロールボリューム全体での対流による内部エネルギーの出入は次式で表される2.21
式変形の詳細は式(A.8)
 に示す。
に示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.22
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.23
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
時間あたりの仕事(仕事率)は面に作用する力(応力と面積の積)と速度の内積で表される2.24
仕事と仕事率は次式のように表される。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから外への作用が負、内への作用が正になるように符号を加え、向かい合う面を足し合わせる2.25
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリューム内に作用するため内部のエネルギー量が増え、負の方向で外へ作用するためエネルギー量が減るのでそのままでよい。しかし、右の面では正の方向で外に作用するためエネルギー量が減り、負の方向で内に作用するためエネルギー量が増えるので負号
軸の正の方向でコントロールボリューム内に作用するため内部のエネルギー量が増え、負の方向で外へ作用するためエネルギー量が減るのでそのままでよい。しかし、右の面では正の方向で外に作用するためエネルギー量が減り、負の方向で内に作用するためエネルギー量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.26
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)、下付きを外す。コントロールボリューム全体での対流による成分の質量の出入は次式で表される2.27
式変形の詳細は式(A.10)
 に示す。
に示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.28
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.29
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)、下付きを外す。コントロールボリューム全体での拡散による成分の質量の出入は次式で表される2.30
式変形の詳細は式(A.11)
 に示す。
に示す。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.31
例えば 軸に垂直な左の面では
軸に垂直な左の面では 軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号
軸の正の方向でコントロールボリュームに入るため内部の量が増え、負の方向で出て行くため量が減るのでそのままでよい。しかし、右の面では正の方向で出て行くため量が減り、負の方向で入るため量が増えるので負号 を加え逆にする。
を加え逆にする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
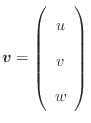
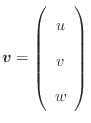
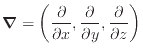
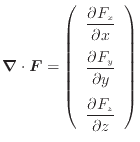 である。
である。