

Next: 2 なぜ対数グラフを使うのか
Up: 対数グラフ
Previous: 対数グラフ
何のために対数グラフのようなややこしいグラフを使うのか解説する。対数グラフの特徴的な対数軸について述べた後に、対数グラフの特徴を示す。
通常のグラフと対数グラフの違いは、対数グラフではグラフの軸の片方もしくは両方の軸の値と長さの関係が対数となっていることである。通常使われるグラフ(線形グラフ)では、グラフの値と長さの関係が線形となっている。
グラフの値と長さの関係について、線形の場合(通常のグラフ)と対数の場合(対数グラフ)について、一つの軸だけを取り出して考えてみる。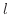 と
と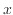 の関係が線形であれば定数
の関係が線形であれば定数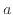 と
と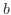 により次式で表される。
により次式で表される。
グラフ上に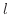 と
と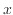 の関係を描くと直線となる。
軸の値
の関係を描くと直線となる。
軸の値
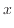 値
と長さ
値
と長さ
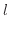 長さ
が線形の関係の場合は、定数
長さ
が線形の関係の場合は、定数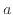 と
と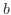 により
により
と表すことが出来る。
普通(線形の関係)のグラフの軸を描いてみよう。例えば、軸の中の長さが5 cmで値が0 ? 10とすると、図1の様に左端から0.5 cmごとに値が1増える。
この時、値
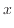 値
と長さ
値
と長さ
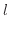 長さ
の関係は次のように線形となる。
長さ
の関係は次のように線形となる。
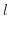 長さ 長さ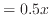 値 値 |
|
同じながさが5cmの軸に5 ? 25の値を入れると、図2の様に左端から0.25cmごとに値が1増える。
この時、値
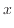 値
と長さ
値
と長さ
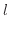 長さ
の関係は次のように線形となる。
長さ
の関係は次のように線形となる。
もう一つ、同じながさが5cmの軸に1 ? 100の値を入れると、図3の様に左端から 5/99 cmごとに値が1増える。
この時、値
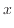 値
と長さ
値
と長さ
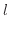 長さ
の関係は次のように線形となる。
長さ
の関係は次のように線形となる。
次は値
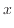 値
と長さ
値
と長さ
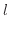 長さ
の関係が対数の軸を書いてみる。対数の関係とは、
長さ
の関係が対数の軸を書いてみる。対数の関係とは、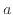 と
と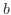 、
、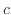 を定数としたとき、
を定数としたとき、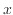 と
と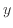 の関係が対数であれば、
の関係が対数であれば、
で表すことの出来る関係である。グラフの対数軸では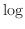 の底である
の底である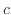 には10を用いる。
値
には10を用いる。
値
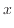 値
と長さ
値
と長さ
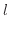 長さ
が対数の関係の場合は、定数
長さ
が対数の関係の場合は、定数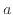 と
と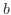 により
により
と表すことが出来る。ここで
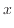 値
と長さ
値
と長さ
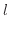 長さ
の関係は対数であるが、
長さ
の関係は対数であるが、
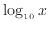 値
と長さ
値
と長さ
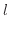 長さ
の関係は線形となっている。
対数(の関係)のグラフの軸を描いてみる。図1の値の0は対数をとることが出来ないので、図3と同じ値で、長さが5cmの軸で1 ? 100の値を対数の関係で入れると、図4の様になる。
この時、値
長さ
の関係は線形となっている。
対数(の関係)のグラフの軸を描いてみる。図1の値の0は対数をとることが出来ないので、図3と同じ値で、長さが5cmの軸で1 ? 100の値を対数の関係で入れると、図4の様になる。
この時、値
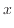 値
と長さ
値
と長さ
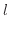 長さ
の関係は次のような対数の関係となる。
長さ
の関係は次のような対数の関係となる。
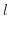 長さ 長さ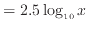 値 値 |
|
値が1の時は 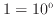 であるので、長さは
であるので、長さは
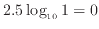 左端の位置となる。
値が2の時は、
左端の位置となる。
値が2の時は、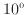 の隣の目盛で、長さは
の隣の目盛で、長さは
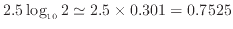 となる。図4でも赤点線で示すように2の目盛は左端から0.75 cmあたりに位置していることが確認できる。
値が11の時には、1から目盛が1ずつ増えてきているので、10の目盛の右隣と考えたいが、幅が大きく変わっている。11の時の長さを計算すると、
となる。図4でも赤点線で示すように2の目盛は左端から0.75 cmあたりに位置していることが確認できる。
値が11の時には、1から目盛が1ずつ増えてきているので、10の目盛の右隣と考えたいが、幅が大きく変わっている。11の時の長さを計算すると、
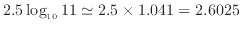 であり、10の目盛の左端からの長さが2.5 cmであるので、図4の青鎖線で示すように約0.1cm左にずれただけである。対数軸では桁が変わった後も同じ間隔で目盛をふると、目盛の数が非常に多くなってしまうため、桁が一つ上がると目盛間隔も一桁増やす。この場合は目盛間隔が1から10に変わり、10の値の次の目盛は20となる。
であり、10の目盛の左端からの長さが2.5 cmであるので、図4の青鎖線で示すように約0.1cm左にずれただけである。対数軸では桁が変わった後も同じ間隔で目盛をふると、目盛の数が非常に多くなってしまうため、桁が一つ上がると目盛間隔も一桁増やす。この場合は目盛間隔が1から10に変わり、10の値の次の目盛は20となる。
同じ長さが5cmの軸に図2と同様に5-25を対数の関係で入れると、図5の様になる。
この時、値
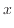 値
と長さ
値
と長さ
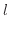 長さ
の関係は次のような対数の関係となる。
長さ
の関係は次のような対数の関係となる。


Next: 2 なぜ対数グラフを使うのか
Up: 対数グラフ
Previous: 対数グラフ
関連する記事
・この記事の新しい版
対数グラフ 2020.03.25版
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版はhttp://camellia.thyme.jpで公開している。
![]() と
と![]() の関係が線形であれば定数
の関係が線形であれば定数![]() と
と![]() により次式で表される。
により次式で表される。
![]() 値
と長さ
値
と長さ
![]() 長さ
の関係が対数の軸を書いてみる。対数の関係とは、
長さ
の関係が対数の軸を書いてみる。対数の関係とは、![]() と
と![]() 、
、![]() を定数としたとき、
を定数としたとき、![]() と
と![]() の関係が対数であれば、
の関係が対数であれば、
![]() 値
と長さ
値
と長さ
![]() 長さ
の関係は次のような対数の関係となる。
長さ
の関係は次のような対数の関係となる。