A..2.1 指数の変形

Next: A..2.2 積の変形 Up: A..2 logの変形 Previous: A..2 logの変形

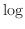$\log$ の指数は次式のように前に出すことができる。

$\displaystyle \log_a b^c = c \log_a b$

これは、

$\displaystyle b = a^n$

となる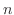

が存在するとき、次式が成り立つ。

$\displaystyle \log_a b = \log_a a^n = n$

このことから次のように導くことができる。

$\displaystyle \log_a b^c$	$\displaystyle = \log_a ( a^n )^c$
	$\displaystyle = \log_a a^{nc}$
	$\displaystyle = nc$ （ $\displaystyle \log_a b = n$ であるので）
	$\displaystyle = c \log_a b$

例えば、

$\displaystyle \log_2 8^2 = \log_2 2^{3 \times 2} = 3 \times 2 \log_2 2$

となる。

Next: A..2.2 積の変形 Up: A..2 logの変形 Previous: A..2 logの変形

関連する記事