• 学問 -top-

＜戻る: 1 対数グラフと線形グラフの性質＞   ＜次へ: 2.2 対数軸＞

2 対数グラフの軸

対数グラフの特徴的な対数軸について述べる。 通常の線形グラフと対数グラフの違いは、対数グラフではグラフの軸の片方もしくは両方の軸が値と長さの関係が対数である対数軸となっていることである。通常使われるグラフ（線形グラフ）では、グラフの値と長さの関係が線形となっている。通常使われる線形の関係の線形軸と対数の関係の対数軸についてそれぞれ説明する。

2.1 線形軸

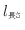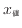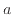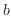グラフの値と長さの関係について、線形の場合（通常のグラフ）の軸である線形軸を考えてみる。左端からの長さ $l_{\rm 長さ}$ と軸の値 $x_{\rm 値}$ の関係が線形であれば定数$a$ と$b$ により次式で表される。

$$l_{長さ} = ax_{値} + b$$

普通（線形の関係）のグラフの軸を描いてみよう。例えば、軸の中の長さが5 cmで値が0 ? 10とすると、図5の様に左端から0.5 cmごとに値が1増える。 この時、値 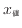$x_{\rm 値}$ と左端からの長さ 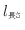$l_{\rm 長さ}$ の関係は次のように線形となる。

$$l_{\rm 長さ} = 0.5 x_{\rm 値}$$

同じながさが5cmの軸に5～25の値を入れると、図6の様に左端から0.25cmごとに値が1増える。

図 5: 線形グラフの軸 1

図 6: 線形グラフの軸 2

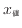この時、値 $x_{\rm 値}$ と左端からの長さ 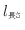$l_{\rm 長さ}$ の関係は次のように線形となる。

$$l_{\rm 長さ} = 0.25 x_{\rm 値} - 1.25$$

もう一つ、同じながさが5cmの軸に1～100の値を入れると、図7の様に左端から 5/99 cmごとに値が1増える。 この時、値 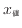$x_{\rm 値}$ と長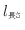さ $l_{\rm 長さ}$ の関係は次のように線形となる。

$$l_{\rm 長さ} = 5/99 x_{\rm 値} - 5/99$$

図 7: 線形グラフの軸 3

＜戻る: 1 対数グラフと線形グラフの性質＞   ＜次へ: 2.2 対数軸＞

• 学問 -top-

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camelllia.netで公開している。