<戻る: 2.1 線形軸>
<次へ: 3 対数グラフでの変化>
次は値
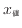 と長さ
と長さ
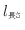 の関係が対数の軸を書いてみる。
グラフの対数軸では
の関係が対数の軸を書いてみる。
グラフの対数軸では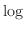 の底には10を用いる2。
対数軸では値
の底には10を用いる2。
対数軸では値
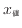 と左端からの長さ
と左端からの長さ
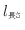 が定数
が定数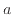 と
と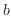 により
により
と表すことが出来る
3。
前節2.1の線形軸と同じ値で対数軸を描こう。図5の値の0は対数をとることが出来ないので、図7と同じ長さが5cmの軸で1 ? 100の値を対数の関係で入れると、図8の様になる。
この時、値
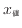 と左端からの長さ
と左端からの長さ
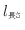 の関係は次のような対数の関係となる。
の関係は次のような対数の関係となる。
値
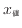 が1の時は
が1の時は 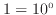 、
、
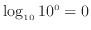 であるので、長さは
であるので、長さは
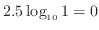 左端の位置となる。
値
左端の位置となる。
値
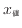 が2の時(
が2の時(
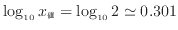 )は、
)は、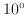 の隣の目盛で、長さは
の隣の目盛で、長さは
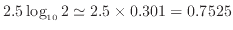 となる。図8でも赤点線で示すように2の目盛は左端から0.75 cmあたりに位置していることが確認できる。
値が11の時には、1から目盛が1ずつ増えてきているので、10の目盛の右隣と考えたいが、10を境に幅が大きく変わる。11の時の長さを計算すると、
となる。図8でも赤点線で示すように2の目盛は左端から0.75 cmあたりに位置していることが確認できる。
値が11の時には、1から目盛が1ずつ増えてきているので、10の目盛の右隣と考えたいが、10を境に幅が大きく変わる。11の時の長さを計算すると、
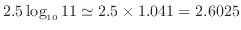 であり、10の目盛の左端からの長さが2.5 cmであるので、図8の青鎖線で示すように約0.1cm左にずれただけである。対数軸では桁が変わった後も同じ間隔で目盛をふると、目盛の数が非常に多くなってしまうため、桁が一つ上がると目盛間隔も一桁増やす。この場合は目盛間隔が1から10に変わり、10の値の次の目盛は20となる。<図中の灰色の軸が前節で示した
であり、10の目盛の左端からの長さが2.5 cmであるので、図8の青鎖線で示すように約0.1cm左にずれただけである。対数軸では桁が変わった後も同じ間隔で目盛をふると、目盛の数が非常に多くなってしまうため、桁が一つ上がると目盛間隔も一桁増やす。この場合は目盛間隔が1から10に変わり、10の値の次の目盛は20となる。<図中の灰色の軸が前節で示した 、
、 であり、おまけで計算しているように、傾きや切片はこの軸から読み取ると元の関数を求めることができる。>
であり、おまけで計算しているように、傾きや切片はこの軸から読み取ると元の関数を求めることができる。>
同じ長さが5cmの軸に図6と同様に5~25を対数の関係で入れると、図9の様になる。
この時、値
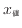 と長さ
と長さ
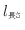 の関係は次のような対数の関係となる。
の関係は次のような対数の関係となる。
脚注
- ...の底には10を用いる2
- 常用対数と呼ぶ。
- ...
と表すことが出来る3
- ここで
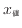 と長さ
と長さ
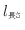 の関係は対数であるが、(
の関係は対数であるが、(
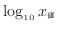 )と長さ
)と長さ
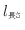 の関係は線形となっている。
の関係は線形となっている。
<戻る: 2.1 線形軸>
<次へ: 3 対数グラフでの変化>
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camelllia.netで公開している。
![]() と長さ
と長さ
![]() の関係は次のような対数の関係となる。
の関係は次のような対数の関係となる。