<戻る: 2 具体的な例>
<次へ: 4 熱も状態量ではない>
前節のように経路が単純な過程の組み合わせでない場合には、経路全体を積分し仕事を求める。積分するには経路を指定した経路積分が必要であり、計算の際には媒介変数が用いられる。
媒介変数として時間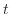 1s (単位:無次元)
[s]
を取り具体的な計算をしてみる。
体積
1s (単位:無次元)
[s]
を取り具体的な計算をしてみる。
体積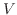 は次式のように初め3.0
は次式のように初め3.0 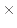 10
10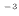 m
m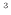 (3.0 リットル)で1 s毎に0.1
(3.0 リットル)で1 s毎に0.1 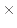 10
10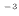 m
m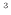 圧縮される。
圧縮される。
圧力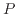 は1.0
は1.0 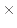 10
10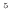 Pa(約一気圧)から次式脚注4のように増えていくとする。
Pa(約一気圧)から次式脚注4のように増えていくとする。
式(11)に示すように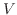 は
は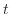 のみの一変数関数として表されている。
のみの一変数関数として表されている。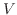 の
の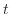 での微分を求める。
での微分を求める。
仕事の微小量を求める式(10)に式(12)と式(13)を代入して0 sから
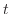 f
まで経路積分をする。経路中にされた仕事を求めたいので、0 sでの仕事は0 Jである。
f
まで経路積分をする。経路中にされた仕事を求めたいので、0 sでの仕事は0 Jである。
この変化を前節と同じように図2に表す。状態の変化に対して仕事が線で表される。
脚注4 二原子分子の理想気体が可逆断熱変化したと仮定し、「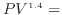 一定」の関係を用いる。
一定」の関係を用いる。
<戻る: 2 具体的な例>
<次へ: 4 熱も状態量ではない>
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camelllia.netで公開している。
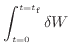
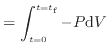
![$\displaystyle = \int^{t_\text{f}}_0 - [(29.37 \text{m$^{4.2}$\ Pa}) \; \{-(0.1 ...
... 3 \times 10^{-3} \; {\rm m^3}\}^{-1.4} ] (- 0.1 \; {\rm m^3/s} \; \mathrm{d}t)$](img54.png)
![$\displaystyle = \int^{t_\text{f}}_0 [(2.937 \text{ m$^{7.2}$\ Pa/s}) \; \{-(0.1...
...3/s})t + 3 \times 10^{-3} \; {\rm m^3}\}^{-1.4} ] \; {\rm m^3/s} \; \mathrm{d}t$](img55.png)
![$\displaystyle = \left[ \frac{2.937 \text{ m$^{7.2}$\ Pa/s}}{(-0.1 \times 10^{-3...
...; {\rm m^3/s})t + 3 \times 10^{-3} \; {\rm m^3}\}^{-0.4} \right]^{t_\text{f}}_0$](img56.png)