熱伝導率と熱拡散率（温度伝導率）の違い

熱伝導率 Thermal conductivity [W/(m K)]と熱拡散率（熱拡散係数、温度伝導率、温度拡散率とも呼ばれる） Thermal diffusivity [m/s²]はともに物質と状態が決まれば値が決まる物性値である。流体（気体と液体）の粘性を表す粘性係数（粘度） Dynamic viscosityと動粘性係数（動粘度） Kinematic viscosityの関係に近い。

熱伝導率は熱の伝わりやすさを表し単位はW/(m K)である。温度勾配に応じて内部エネルギーが熱として拡散する。拡散は温度勾配によって起こるため、温度場へ拡散が与える影響は温度の変化のし易さを表す熱拡散率（温度伝導率）として表される。熱拡散率（温度伝導率）は温度の伝わり易さ（拡散）を表しており、単位はm²/sである。

熱伝導率は次式で表されるフーリエの法則で定義され、温度勾配に対して伝熱量の関係を表す。

$\displaystyle Q = - A k \dfrac{\partial T}{\partial x}$

(1)

ここでQ [W]は伝熱量、A [m²]は熱の伝わる面積、k [W/(K m)]は熱伝導率、T [K]は温度、x [m]は位置を表す。熱拡散率a [m²/s]は熱伝導率k [W/(K m)]を比熱c [J/(K kg)]と密度ρ [kg/m³]で割ることで求められる。

$\displaystyle a = \frac{k}{\rho c}$

(2)

熱拡散率（温度伝導率）と温度勾配との関係を考えるために、図1のように体積$V$[m³]のある微少な領域を考え、表面積A[m²]で周囲と温度勾配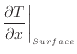 $\dfrac{\partial T}{\partial x} \bigg \vert _{Surface}$ [K/m]で接しているとする。そこで温度がどの程度時間的に変化し易いかと熱拡散率の関係を考える。伝わった熱によってどれくらい温度が変化するかは、領域を単位温度上げるのに必要なエネルギーで伝わった熱を割ればよい。領域を単位温度上げるのに必要なエネルギーは領域の密度と比熱、体積ρ c V [J/K]をかけると求められる。そこで式(1)の両辺を密度×比熱×体積（ρ c V ）[J/K]で割る。

$\displaystyle \dfrac{Q}{\rho c V}$

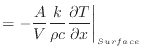
$\displaystyle = - \dfrac{A}{V} \dfrac{k}{\rho c}\dfrac{\partial T}{\partial x} \bigg \vert _{Surface}$

(3)

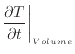また、伝熱量Q [W]は、対象領域での内部エネルギーの時間変化量に等しいので、温度の時間変化 $\dfrac{\partial T}{\partial t} \bigg \vert _{Volume}$ [K/s]と次の関係にある。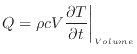

$\displaystyle Q = \rho c V \dfrac{\partial T}{\partial t} \bigg \vert _{Volume}$

(4)

式(2)と上式(4)を(3)に代入する。

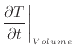
$\displaystyle \dfrac{\partial T}{\partial t} \bigg \vert _{Volume}$

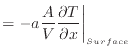
$\displaystyle = - a \dfrac{A}{V} \dfrac{\partial T}{\partial x} \bigg \vert _{Surface}$

(5)

このように熱拡散率a [m²/s]が大きくなると温度の時間変化が大きくなることをフーリエの法則から示すことができる。

$\includegraphics[width=50mm]{figures/Diffusivity.eps}$
図1 対象領域

熱伝導率と熱拡散率（温度伝導率）の関係を分かり易く想像するために、水槽に貯まる水の量と水位に例える。図2のように細長い水槽が並んでいて左から水が入り、水槽の間の壁には穴があいていて隣の水槽に水が流れ込む水槽の列を考える。流れてくる水の量が伝熱量（伝わる熱の量）に、水槽の水位の変化が温度の変化に対応する。水槽の奥行きが比熱×密度に対応し、奥行きが深いと水が貯まっても水位は変化しづらい。温度差が増えると伝わる熱の量も増えるように、水位の差が大きいと流れ込む水の量も増える。熱伝導率は温度差（温度勾配）に対しての熱の伝わりやすさであり、水槽で考えると水位差に対してどれだけ水が流れ込むか、すなわち水槽の間の穴の数となる。それに対して熱拡散率（温度伝導率）は熱伝導率を比熱×密度で割った値であり温度の伝わりやすさを表しているので、水槽であれば穴の大きさを水槽の奥行きで割った値であり水位の変わり易さを表している。穴が大きくても水槽の奥行きが深ければ水が多く流れ込んでも水位の変化が小さいので次の水槽へは流れ込みにくい。奥行きが浅ければ、少ない流量でも水位がすぐにあがるため次の水槽へ流れ込みやすく、水がより短い時間で遠くの水槽まで伝わる。

$\includegraphics[width=100mm]{figures/tank.eps}$
図2 水槽での比喩

2013年11月27日　椿耕太郎

熱伝導率と熱拡散率（温度伝導率）の違い

関連する記事