粘性係数（粘度）と動粘性係数（動粘度）の違い

粘性係数（粘度） Dynamic viscosityと動粘性係数（動粘度） Kinematic viscosityはともに物質と状態が決まれば値が決まる物性値である。流体（気体と液体）の性質を表す。流体の流れがあり、その中で速度に違いがあると、下図に示すように速度が速い流体を遅く、速度の遅い流体を早くする方向に粘性力が働く。

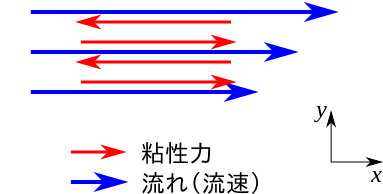
このときに流体間に働く力は単位面積あたりの応力τ [N/m²]として速度v [m/s]の勾配と粘性係数μ [Pa s]より次式のように表される。

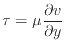
$\displaystyle \tau = \mu \frac{\partial v}{\partial y}$

粘性係数はある物質がどれくらい力を拡散しやすいかを表していて、動粘性係数はある物質がどれくらい速度を拡散しやすいかを表している。力の拡散と速度の拡散はどう違うのだろうか。粘性係数が大きいと大きな力が伝わるが、物質の質量（密度）が大きければ大きな力が加わっても速度は大きく変化しない。質量（密度）が小さければ大きな力でなくても速度も大きく変化し、遠くまで速度の変化が拡散する。このように速度の伝わりやすさ動粘性係数は力の伝わりやすさ粘性係数と密度によって決まる。このことから動粘性係数ν [m²/s]は次式のように粘性係数μ [Pa s]を密度ρ [kg/m³]で割ることで求まる。

$\displaystyle \nu = \frac{\mu}{\rho}$

熱伝導率と熱拡散率（温度伝導率）も同じ関係で、熱の拡散と温度の拡散をそれぞれ表してる。伝わった熱によってどれくらい温度が変化するかは、体積あたり単位温度上げるのに必要なエネルギーで熱を割ればよい。体積あたりの単位温度上げるのに必要なエネルギーは比熱に密度をかけると求められる。このことから熱伝導率k [W/m K]を比熱c [J/K kg]と密度ρ [kg/m³]で割ると熱拡散率a [m²/s]になる。

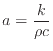
$\displaystyle a = \frac{k}{\rho c}$

運動量（内部エネルギー）が力（熱）として伝わる（拡散する）。運動量（内部エネルギー）の拡散は速度（温度）の勾配があると力（熱）として伝わる。その力（熱）の伝わる大きさが物質により違い、粘性係数（熱伝導率）として表される。拡散は速度（温度）勾配によって起こるため、速度場（温度場）へ拡散が与える影響は速度（温度）の変化を表す動粘性係数（熱拡散率）として表される。動粘性係数と熱拡散率は速度と温度の拡散を表しており、共に単位はm²/sである。

2013年3月26日　椿耕太郎

粘性係数（粘度）と動粘性係数（動粘度）の違い

関連する記事