• 学問 -top-

1.5.3 可逆サイクルでの熱の比

同じ二つの熱源で動作する可逆サイクルは、どんな中身のサイクルでも必ず同じ効率となりサイクルの構成によらない。同じ熱源でなく異なる熱源で動作する可逆サイクルでの効率はどちらが高くなるだろうか。このとき効率は可逆サイクルの構成にはよらないので、効率を決める要素は二つの熱源の条件だけである。熱源の条件としては温度のみ(1.4.3節 p. )であるので、可逆サイクルの効率を決める条件は二つの熱源の温度のみである。温度$T_1$ の熱源１と温度$T_2$ の熱源２で動作する可逆サイクルの効率は二つの熱源の温度（$T_1$ 、$T_2$ ）の関数となる^1.16。

$$\epsilon_{12可} = f(T_1, T_2)$$ (1.18)

この関数 $f(T_1, T_2)$ がどのような関数か明らかにするため、図1.20に示すように、温度$T_H$ の熱源と温度$T_L$ の熱源で動作する可逆サイクル１と温度$T_H$ の熱源と温度$T_M$ の熱源で動作する可逆サイクル２、温度$T_M$ の熱源と温度$T_L$ の熱源で動作する可逆サイクル３を考える。このとき熱源の温度の関係は $T_H > T_M > T_L$ とする。

図 1.20: 可逆サイクルの効率

この場合の各サイクルの効率はサイクルの効率の式(1.12) (p. )と式(1.18)から熱源の温度により次のように表される。

$$\epsilon_{1可} = \frac{ \vert W_{1 可} \vert }{ \vert Q_{1, H 可} \vert } = f(T_H, T_L)$$ (1.19)

$$\epsilon_{2可} = \frac{ \vert W_{2 可} \vert }{ \vert Q_{2, H 可} \vert } = f(T_H, T_M)$$ (1.20)

$$\epsilon_{3可} = \frac{ \vert W_{3 可} \vert }{ \vert Q_{3, M 可} \vert } = f(T_M, T_L)$$ (1.21)

ここで熱力学第一法則、式(1.11) (p. )より

$$\vert Q_{1, H 可} \vert = \vert Q_{1, L 可} \vert + \vert W_{1 可} \vert$$

$$\vert Q_{2, H 可} \vert = \vert Q_{2, M 可} \vert + \vert W_{2 可} \vert$$

$$\vert Q_{3, M 可} \vert = \vert Q_{3, L 可} \vert + \vert W_{3 可} \vert$$

が成り立つ。上3式を左辺の高温側熱源から伝わる熱量で割り、それぞれの効率(式(1.19)-式(1.21))を代入し変形すると以下の関係が成り立つ。

$$\frac{ \vert Q_{1, L 可} \vert }{ \vert Q_{1, H 可} \vert } = 1 - \epsilon_{1可} = 1 - f(T_H, T_L)$$ (1.22)

$$\frac{ \vert Q_{2, M 可} \vert }{ \vert Q_{2, H 可} \vert } = 1 - \epsilon_{2可} = 1 - f(T_H, T_M)$$ (1.23)

$$\frac{ \vert Q_{3, L 可} \vert }{ \vert Q_{3, M 可} \vert } = 1 - \epsilon_{3可} = 1 - f(T_M, T_L)$$ (1.24)

ここで上3式の最右辺も二つの熱源の温度のみの関数となるので、次式のような関数 $g(T_1, T_2)$ をおく。

$$g(T_1, T_2) = 1 - f(T_1, T_2) = \frac{ \vert Q_{2 可}\vert }{ \vert Q_{1 可}\vert }$$ (1.25)

式(1.22)-式(1.24)へ式(1.25)を適用すると、それぞれのサイクルでの高温熱源からの熱と低温熱源からの熱の大きさの比は次のように温度の関数で表される。

$$\frac{ \vert Q_{1, L 可} \vert }{ \vert Q_{1, H 可} \vert } = g(T_H, T_L)$$ (1.26)

$$\frac{ \vert Q_{2, M 可} \vert }{ \vert Q_{2, H 可} \vert } = g(T_H, T_M)$$ (1.27)

$$\frac{ \vert Q_{3, L 可} \vert }{ \vert Q_{3, M 可} \vert } = g(T_M, T_L)$$ (1.28)

サイクル２の低温側の熱源へ伝わる熱の大きさ$Q_{2, M}$ と、サイクル３の高温側の熱源から伝わる熱の大きさ ${Q_{3, M}}$ を、同じ大きさになるよう ^1.17にそれぞれのサイクルを動作させて（ $\vert Q_{2, M 可} \vert = \vert Q_{3, M 可} \vert = \vert Q_{M 可}\vert$ ）、サイクル2とサイクル3を一つのサイクルとして動作させる。サイクル2とサイクル3の熱量の比の積から、次式の関係が成り立つ。

$$\frac{ \vert Q_{M 可} \vert }{ \vert Q_{2, H 可} \vert } \frac{ \... ...t Q_{M 可}\vert } = \frac{ \vert Q_{3, L 可} \vert }{ \vert Q_{2, H 可} \vert }$$ (1.29)

サイクル２とサイクル３を合わせた一つのサイクルとして考えると、温度$T_H$ の熱源と温度$T_L$ の同じ二つの熱源の間で動作する可逆サイクルとみなせるので、サイクル１と効率は等しくなる。効率が等しいので伝わる熱の大きさの比はサイクル１と等しく次式が成り立つ。

$$\frac{ \vert Q_{3, L 可} \vert }{ \vert Q_{2, H 可} \vert } = \frac{ \vert Q_{1, L 可} \vert }{ \vert Q_{1, H 可} \vert }$$ (1.30)

式(1.29)と式(1.30)から次の関係が成り立つ。

$$\frac{ \vert Q_{M 可} \vert }{ \vert Q_{2, H 可} \vert } \frac{ \... ... Q_{M 可}\vert } = \frac{ \vert Q_{1, L 可} \vert }{ \vert Q_{1, H 可} \vert }$$

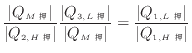
上式の最左辺と最右辺に式(1.26)、式(1.27)、式(1.28)を代入し温度の関数$g$ で表すと、

$$g(T_H, T_M) g(T_M, T_L) = g(T_H, T_L)$$

となる^1.18。ここで、左辺は$T_M$ を含む関数となっているが、右辺は$T_H$ と$T_L$ のみの関数で$T_M$ の関数ではない。そのため、関数$g$ は左辺で$T_M$ が消える形の関数である必要がある。積で$T_M$ が消えるように関数$g$ を、ある温度を表す関数$\phi$ （ファイ）で以下の形で表す。

$$g(T_1, T_2) = \frac{\phi(T_2)}{\phi(T_1)}$$

上式のように関数$g$ が温度の商の関数だと、次式のように$T_M$ が左辺から消える。

$$g(T_H, T_M) g(T_M, T_L) = \frac{\phi(T_M)}{\phi(T_H)} \frac{\phi(T_L)}{\phi(T_M)} = \frac{\phi(T_L)}{\phi(T_H)} = g(T_H, T_L)$$

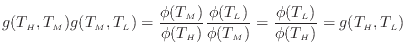
熱源の温度と、熱源とやりとりする熱量の関係をまとめると式(1.25)と式(1.5.3)より

$$\frac{ \vert Q_{2 可} \vert }{ \vert Q_{1 可} \vert } = \frac{\phi(T_2)}{\phi(T_1)}$$ (1.31)

ここで$\phi$ は単一の温度の関数である。上式(1.31)の関係から温度を定義する[3]^1.19。次の式の関係が成り立つように、$T$ をそのまま温度の関数$\phi$ と定義した温度を熱力学的温度（絶対温度）といい単位は[K](ケルビン)で表される。

$$\phi(T) = T$$

また日常使われる摂氏温度$t$ [℃]は次式で表される。

$$\phi(T) = t + 273.15$$

上二式から絶対温度$T$ [K]と摂氏温度$t$ [℃]の関係は次式で表される。

$$T = t + 273.15$$

この熱力学的温度で表現すると、温度$T_1$ と温度$T_2$ の二つの熱源で動作する可逆サイクルの熱源とやりとりする熱量$Q_1$ と熱量$Q_2$ の関係は次のように熱力学的温度（絶対温度）の比で表される。

$$\frac{ \vert Q_{2 可} \vert }{ \vert Q_{1 可} \vert } = \frac{T_2}{T_1}$$ (1.32)

$Q_1$ と$Q_2$ は伝わる方向が逆であり、符号が逆となるので絶対値を外して変形し次式となる。

$$\frac{ Q_{1 可} }{ T_1 } = - \frac{ Q_{2 可} }{T_2}$$ (1.33)

式(1.18)p. と式(1.25) p. 、式(1.32)より、温度$T_1$ の熱源と温度$T_2$ の熱源（$T_1 > T_2$ ）で動作する可逆サイクルの熱機関の効率は次式(1.34)で表される。

$$\epsilon_{12可} = 1 - \frac{ \vert Q_{2 可} \vert }{ \vert Q_{1 可} \vert } = 1 - \frac{T_2}{T_1} = \frac{T_1 - T_2}{T_1}$$ (1.34)

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。